I was reading Constraint Satisfaction Problem chapter from Artificial Intelligence 3rd ed book by Peter Norvig et al. On page 219, section 6.3 it explains computation of conflict set for conflict directed backjumping as follows:
In our example, $SA$ fails, and its conflict set is (say) $\{WA, NT,Q\}$. We backjump to $Q$,and $Q$ absorbs the conflict set from $SA$ (minus $Q$ itself, of course) into its own direct conflict set, which is $\{NT, NSW\}$; the new conflict set is $\{WA, NT, NSW\}$. That is, there is no solution from $Q$ onward, given the preceding assignment to $\{WA, NT, NSW\}$. Therefore, we backtrack to $NT$, the most recent of these. NT absorbs $\{WA, NT, NSW\}−\{NT\}$ into its own direct conflict set $\{WA\}$,giving $\{WA, NSW\}$ (as stated in the previous paragraph). Now the algorithm backjumps to $NSW$, as we would hope.
To summarize: let $X_j$ be the current variable, and let $conf(X_j)$ be its conflict set. If every possible value for $X_j$ fails, backjump to the most recent variable $X_i$ in $conf(X_j)$, and set
$conf(X_i) ← conf(X_i) ∪ conf(X_j) −\{X_i\}$.
I didn't get the line:
Therefore, we backtrack to $NT$, the most recent of these.
How is $NT$ most recent of $Q$'s conflict set $\{WA,NT,NSW\}$?
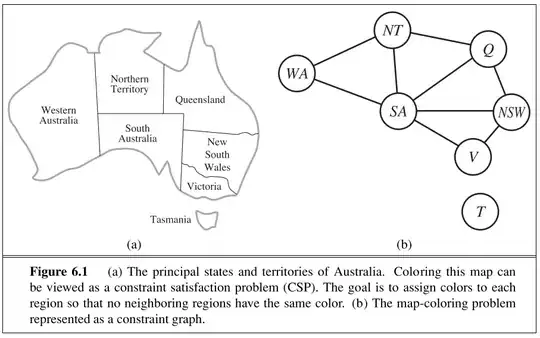
PS: Here is the map coloring example the book discusses: