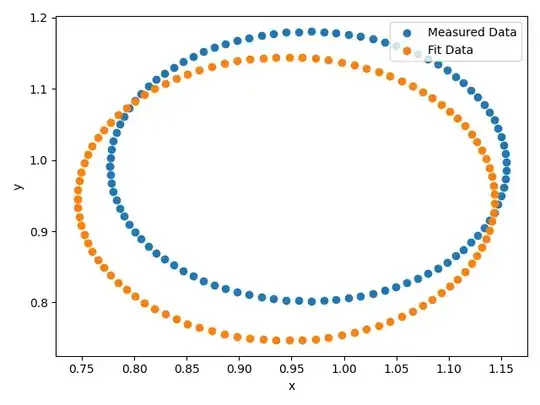
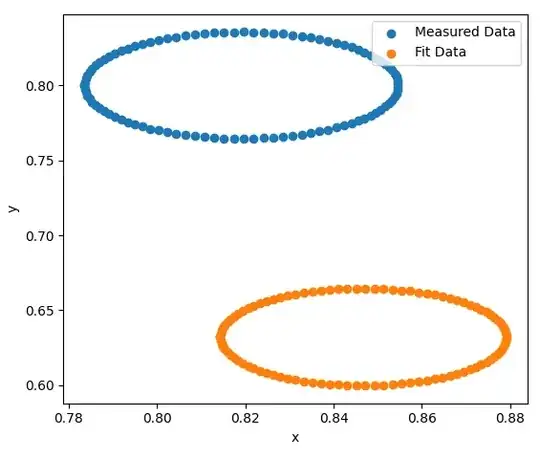
I'm trying to make a neural network in pytorch that picks the parameters of a nonlinear function, the radius and (x,y) center of a circle in the example below, based on a sample of values from the nonlinear function.
More concretely, the neural network trained in the code below takes as input 100 (x,y) points on a circle and outputs radius, x_center, y_center of the circle.
I don't consider this a very difficult problem, but the trained neural network doesn't work very well, as you can see from two example plots after the code. How can the code be improved?
And in case this informs your recommendation, the goal is not to fit circles, which no one needs a neural network to do. I'm trying to use a neural network to calculate 9 parameters in a nonlinear function taking a single real valued input and outputting a complex number f(t) -> a + b*sqrt(-1). The input into the neural network is 54 complex values, and the output is 9 parameter values. I am guaranteed that the 54 complex input values can always be well approximated by f(t) with an appropriately picked 9 parameters. The parameters can easily be guessed by a human because different parameters intuitively change the shape of the complex curve, but I've been unable to use a minimization math algorithm for curve fitting. The problem is there are a lot of local minima the minimization algorithms can encounter before reaching the global minimum. The goal of the neural network is to get a good guess of the 9 parameters at the global minimum for a minimization math algorithm to be close to the global minimum initially, and thus converge to the global minimum rather than get stuck at a local minima.
You probably guessed that I know a bit of math, but I don't know much about machine learning. I was able to pick it up pretty quickly because of my math background, but I am severely lacking in practical experience. I don't know what to do at this point other than randomly changing the number of samples on a circle, number of examples circles, adding more layers to the neural network, adding different types of layers to the neural network, changing the loss function, changing the learning rate, changing the optimizer, changing the loss function, et cetera, but I have no method to my madness.
Post Script
I've found someone who did almost what I need. This paper paired with this github repo used 1,000 samples in a set of 100,000 with 1% failure rate, so there's hope. I have to dig deeper for the innards of their neural network training.
import torch
import numpy as np
import math
import matplotlib.pyplot as plt
#circle parameterized by t, < x(t) , y(t) >
t_parameter = np.linspace(-math.pi, math.pi, 100)
#create random radius,(x,y) center or circle paired with points on circle evaluated at all t in t_parameter
examples = 1000
max_radius = 4
random_rxy = np.random.rand(examples,3)
input_list = []
for i in range(examples):
r_rand = random_rxy.item(i,0) * max_radius
x_rand = random_rxy.item(i,1) * 7 - 2 #-2 < x_rand < 5
y_rand = random_rxy.item(i,2) - 2 #-2 < y_rand < -1
x_coordinates = [r_rand*math.cos(t) + x_rand for t in t_parameter]
y_coordinates = [r_rand*math.sin(t) + y_rand for t in t_parameter]
input_list.append(x_coordinates + y_coordinates)
input_tensor = torch.Tensor(input_list)
output_tensor = torch.Tensor(random_rxy)
print(input_tensor)
'''
tensor([[ x_0_0, x_0_1, ..., x_0_99, y_0_0, y_0_1, ..., y_0_99 ],
[ x_1_0, x_1_1, ..., x_1_99, y_1_0, y_1_1, ..., y_1_99 ],
[ x_2_0, x_2_1, ..., x_2_99, y_2_0, y_2_1, ..., y_2_99 ],
...,
[ x_997_0, x_997_1, ..., x_997_99, y_997_0, y_997_1, ..., y_997_99 ],
[ x_998_0, x_998_1, ..., x_998_99, y_998_0, y_998_1, ..., y_998_99 ],
[ x_999_0, x_999_1, ..., x_999_99, y_999_0, y_999_1, ..., y_999_99 ]])
'''
print(output_tensor) #radious, x circle center, y circle center
'''
tensor([[r_0, x_0, y_0 ],
[r_1, x_1, y_1 ],
[r_2, x_2, y_2 ],
...,
[r_997, x_997, y_997],
[r_998, x_998, y_998],
[r_999, x_999, y_999]])
'''
#define model and loss function.
model = torch.nn.Sequential(
torch.nn.Linear(200, 200),
torch.nn.Tanh(),
torch.nn.Tanh(),
torch.nn.Linear(200, 3)
)
loss_fn = torch.nn.MSELoss(reduction='mean')
#train model
learning_rate = 1e-4
optimizer = torch.optim.Adagrad(model.parameters(), lr=learning_rate)
for t in range(10000):
# Forward pass: compute predicted y by passing x to the model.
output_pred = model(input_tensor)
# Compute and print loss.
loss = loss_fn(output_pred, output_tensor)
if t % 100 == 99:
print(t, loss.item())
'''
99 0.0337635762989521
199 0.0285916980355978
299 0.025961756706237793
399 0.024196302518248558
499 0.022839149460196495
...
9799 0.004136151168495417
9899 0.0040830159559845924
9999 0.004030808340758085
'''
#typical procedure
optimizer.zero_grad()
loss.backward()
optimizer.step()
print(output_tensor[0].tolist())
print(output_pred[0].tolist())
#[0.7722834348678589, 0.46600303053855896, 0.5080233812332153 ]
#[0.7921068072319031, 0.46946045756340027, 0.49222415685653687]
plt.xlabel('x')
plt.ylabel('y')
r_rand, x_rand, y_rand = output_tensor[0].tolist()
plt.scatter([r_rand*math.cos(t) + x_rand for t in t_parameter],[r_rand*math.sin(t) + y_rand for t in t_parameter],label="Measured Data")
r_rand, x_rand, y_rand = output_pred[0].tolist()
plt.scatter([r_rand*math.cos(t) + x_rand for t in t_parameter],[r_rand*math.sin(t) + y_rand for t in t_parameter],label="Fit Data")
plt.legend(loc='upper right')
plt.tight_layout()
plt.show()