Where does the so-called 'loss' / 'loss function' fit into the idea of a perceptron / artificial neuron (as presented in the figure)?

Question

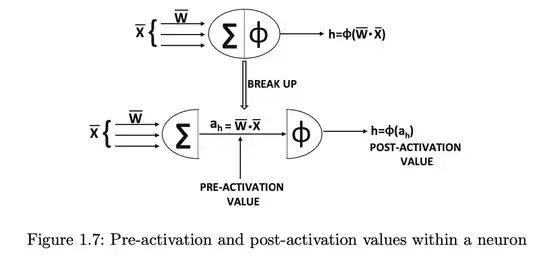
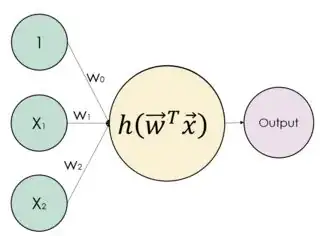
I am currently studying the textbook Neural Networks and Deep Learning by Charu C. Aggarwal. Chapter 1.2.1.3 Choice of Activation and Loss Functions presents the following figure:

$\overline{X}$ is the features, $\overline{W}$ is the weights, and $\phi$ is the activation function.

So this is a perceptron (which is a form of artificial neuron).

But where does the so-called 'loss' / 'loss function' fit into this? This is something that I've been unable to reconcile.

---

EDIT

The way the loss function was introduced in the textbook seemed to imply that it was part of the architecture of the perceptron / artificial neuron, but, according to hanugm's answer, it is external and instead used to update the weights of the neuron. So it seems that I misunderstood what was written in the textbook.

In my question above, I pretty much assumed that the loss function was part of the architecture of the perceptron / artificial neuron, and then asked how it fit into the architecture, since I couldn't see any indication of it in the figure.

Is the loss / loss function part of the architecture of a perceptron / artificial neuron? I cannot see any indication of a loss / loss function in figure 1.7, so I'm confused about this. If not, then how does the loss / loss function relate to the architecture of the perceptron / artificial neuron?

Answer 1

Loss function is a function used to measure the loss. It is not used in any component of a neuron. It is used in updating the weights of the neuron i.e., in order to train the neuron.

The contribution of a loss function is in the updation of $\bar{W}$.

For a given $\bar{X}$ and $\bar{W}$, the neuron gives a post-action value $h$. But the desired output may not be exactly $h$. The distance measure between the desired value (say $h^\prime$) and post-activation value $h$ is called the loss of the perceptron for $\bar{X}$.

We want to decrease the loss of the perception i.e., $\left\vert h - h^\prime \right\vert$. The only task we can do is changing $\bar{W}$, the parameters of the perceptron model given in the question. In order to update the weights, we have to calculate the derivative of loss function wrt the weights of the model and then update weights using some updation rule.

Thus, loss function will come into play during the training phase of the neuron.

To be concise: currently you are dealing with the neuron and its components. Loss functions for training the neuron will come later.

Answer 2

The loss function is simply a way to measure how wrong a neural network is, it doesn't affect the output of the neuron.

Say we have a neural network with 3 output neurons that attempts to classify images of cats, dogs, and humans. The output it gives is the confidence of the neural network's classification. For example if the output is [0, 0.2, 0.8] (0 being the output of the 1st neuron, 0.2 of the 2nd, and 0.8 of the 3rd), this means that the neural network thinks that the image has 0% probability of being a cat, 20% of being a dog and 80% of being a human.

Imagine that the image that was shown to the network is a human, we can say that the target values are [0, 0, 1] because we want it to output that the image is a human with 100% confidence. Now we must measure how wrong the prediction actually was using a loss function. There are many loss functions, but for simplicity I'll use the squared error. In this case the loss will be equal to (1-0.8)^2=0.04 (expected value - output)^2.

The closer the output is to 1, the result inside of the brackets will be closer to 0, so the loss will be smaller. The objective is to minimize this loss function. For example, if the output was 1 instead of 0.8, the network's loss will be (1-1)^2 = 0. If the output was 0.2 instead, the loss would be (1-0.2)^2 = 0.64, which is larger than the two previous, as it is 'more wrong'.

To train the network we use this instead of accuracy for the following reason. With both these outputs [0, 0.1, 0.9], [0.2, 0.3, 0.5] the network predicts 'human', the largest value, but in the first case it is 90% sure whereas in the second it is only 50% sure. We can say that the first network is better, but if we only used accuracy, as both predict the same, they would appear to be just as good.

The same happens when they make a mistake. If the expected values are [0, 1, 0] and one model predicts [0.5, 0.4, 0.1] and the other predicts [0.9, 0, 0.1], they both got it wrong, but the first one was less wrong. The first loss would be (1-0.4)^2 = 0.36 and the second would be (1-0)^2 = 1, which is much higher

Answer 3

Assume we have a binary classification problem, which we want to solve with a simple single-layer perceptron. For a 2d space, a perceptron will have 2 inputs $x_1$ and $x_2$, and a bias denoted $x_0$ which is always $x_0=1$. It also has corresponding learnable weights $w_0$, $w_1$ and $w_2$.

This can be vectorized:

$$ \overline{x} = \begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix}; \ \overline{w} = \begin{bmatrix} w_0 \\ w_1 \\ w_2 \end{bmatrix} $$

Then the pre-activation function $a = \overline{w}\cdot\overline{x}$ nothing more than a linear equation and can be unfolded to $a = w_0 + w_1x_1+w_2x_2$.

In the simplest case $h$ can be defined as follows:

$$h = \begin{cases} \text{class 1} & \text{if $a>0$}\\ \text{class 2} & \text{otherwise} \end{cases} $$

or it can also be defined as $h=\text{sign}(\overline{w}\cdot\overline{x})$, which means that samples above the line belong to class 1.

Since our $h$ is not continuous and not differentiable, we cannot apply gradient descent optimization. Instead, the weights can be optimized iteratively:

for the details, you can refer to Wikipedia

So answering your question, for this particular case, there is no loss function. Optimization of a loss function usually involves SGD which requires the function to be continuous and differentiable. For instance, if $h$ is defined as a sigmoid function, you can use binary cross-entropy as a loss function.

There are also other optimization approaches, such as genetic algorithm, expectation-maximization and hill-climbing that do not require a loss function.