Suppose, I have a problem, where there is rather a small number of training samples, and transfer learning from ImageNet or some huge NLP dataset is not relevant for this task.
Due to the small number of data, say several hundred samples, the use of a large network will very probably lead to overfitting. Indeed, various regularization techniques can partly solve this issue, but, I suppose, not always. A small network will not have much expressive power, however, with the use of Bayesian approaches, like HMC integration, one can effectively obtain an ensemble of models. Provided models in the ensemble are weakly correlated, one can boost the classification accuracy significantly.
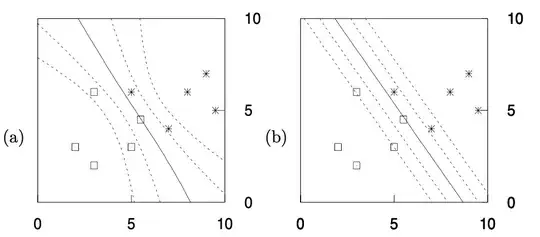
Here I provide the picture from Mackay's book "Information Theory Inference and Learning Algorithms". The model under consideration is single layer neural network with a sigmoid activation function: $$ y(x, \mathbf{w}) = \frac{1}{1 + e^{-(w_0 + w_1 x_1 + w_2 x_2)}} $$
On the left picture, there is a result of Hamiltonian Monte Carlo after a sufficient number of samples, and, on the right, there is an optimal fit.
Integration over the ensemble of models produces a nonlinear separating boundary for NN.
I wonder, can this approach be beneficial for some small-size problems, but not toy, with real-life applications?