How to check whether my loss function is convex or not?

Question

Loss functions are useful in calculating loss and then we can update the weights of a neural network. The loss function is thus useful in training neural networks.

Consider the following excerpt from this answer

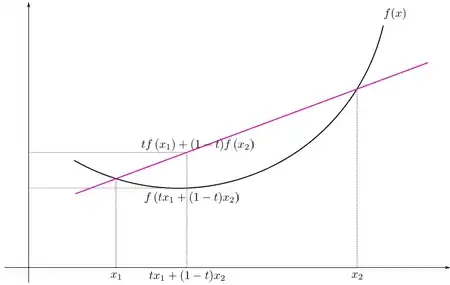
In principle, differentiability is sufficient to run gradient descent. That said, unless $L$ is convex, gradient descent offers no guarantees of convergence to a global minimiser. In practice, neural network loss functions are rarely convex anyway.

It implies that the convexity property of loss functions is useful in ensuring the convergence, if we are using the gradient descent algorithm. There is another narrowed version of this question dealing with cross-entropy loss. But, this question is, in fact, a general question and is not restricted to a particular loss function.

How to know whether a loss function is convex or not? Is there any algorithm to check it?

[Here](https://ai.stackexchange.com/q/11979/2444) is a related question. — nbro, Aug 03 '21 at 13:04

score 1 · Answer 1 · answered Aug 02 '21 at 18:40

1

It is the same as other functions. You can use Theorem 2 in this lecture (from Princeton University):

(ii) condition is about the first-order condition for convexity and (iii) is the second-order. You can also find more detail in chapter 3 of this book ("Convex Optimization" by Stephen Boyd and Lieven Vandenberghe).

answered Aug 02 '21 at 18:40

OmG

1,731
10
19

1

Please check that the lecture page is not accessible. – hanugm Aug 02 '21 at 23:12
@hanugm sorry, I've already checked and I can't see the problem. – OmG Aug 02 '21 at 23:52
1

oh, no problem. It is showing **Error 404 Page Not Found Sorry, the page you are looking for is not available** for me – hanugm Aug 03 '21 at 00:08
@hanugm Sorry, it's strange. By the way, all links work for me. – OmG Aug 03 '21 at 13:21
@OmG It also shows a 404 for me. – Squanchy Jan 20 '23 at 21:17
@Squanchy it's loaded for me. – OmG Jan 21 '23 at 08:13
1

@hanugm I'm not sure what's up with the link... it's strange. If I click it, I indeed also get the error page. But if I then, in my browser, click the address bar and just immediately hit enter again without changing anything, it works fine. Directly copying the URL that OmG provided in their post, and pasting it in my browser, also works fine. So.. I'm not sure how it could be fixed, but it mostly works with a small workaround. – Dennis Soemers Jan 21 '23 at 10:24
There is an issue with the URL encoding it is using %7E instead of ~. You can see the difference in the GET request. This link should work fine https://www.princeton.edu/~aaa/Public/Teaching/ORF523/S16/ORF523_S16_Lec7_gh.pdf – Squanchy Jan 22 '23 at 02:34

score 1 · Answer 2 · edited Aug 03 '21 at 13:38

For the case of at least twice differentiable functions, the answer is given by @OmG - you need to look at the eigenvalues of Hessian.

For the 1-dimensional case the picture is rather intuitive:

If the function grows faster then linear with deviation from the minimum, then the function is convex.

For multidimensional case for any projection on a plane, cutting the loss hypersurface you need to have the same picture as for 1-dimensional case. This is satisfied, provided, that the Hessian matrix is positive definite.

If the function is not twice differentiable, the situation becomes more complicated, and I am not aware of any general algorithm.

However, for the case of piecewise-linear function, you can imagine something like $|x|$, or a more general function like: $$ f(x) = \begin{cases} \alpha x & \alpha > 0, x > 0 \\ \beta x & \beta < 0, x < 0 \end{cases} $$

If any section of the loss hypersurface in the vicinity of such a singularity has this form - the function will be convex as well.

How to check whether my loss function is convex or not?

2 Answers2