Why the partial derivative is $0$ when $F_{ij}^l < 0$?. Math behind style transfer

Question

I am currently in the process of reading and understanding the process of style transfer. I came across this equation in the research paper which went like -

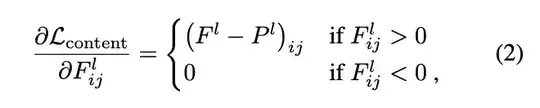
For context, here is the paragraph -

Generally each layer in the network defines a non-linear filter bank whose complexity increases with the position of the layer in the network. Hence a given input image is encoded in each layer of the Convolutional Neural Network by the filter responses to that image. A layer with $N_l$ distinct filters has $N$ feature maps each of size $M$ , where $M_l$ is the height times the width of the feature map. So the re- sponses in a layer l can be stored in a matrix $Fl ∈ R^{N_l×M_l}$ where F l is the activation of the ith filter at position j in ij layer l. To visualise the image information that is encoded at different layers of the hierarchy one can perform gradient descent on a white noise image to find another image that matches the feature responses of the original image (Fig 1, content reconstructions). Let $\vec p$ and $\vec x$ be the original image and the image that is generated, and $P^l$ and $F^l$ their respective feature representation in layer l. We then define the squared-error loss between the two feature representations $\mathcal{L_{content}(\vec p, \vec x, l)} = {1\over 2} \Sigma_{i,j} \big(F_{ij}^l - P_{ij}^l \big)$. The derivative of this loss with respect to the activations in layer $l$ [the equation above $(2)$].

I just want to know why the partial derivative is $0$ when $F_{ij}^l < 0$.

Answer 1

$F_l$ is the activation of the filter. They state in the paper that they base their method on VGG-Network, which uses ReLU as its activation function. In fact, VGG uses it in all of its hidden layers. ReLU is defined as

$$f(x) = max(0,x)$$

Since ReLU is 0 for all x's below 0, the equation above holds; When x is non-positive, all terms in the loss function are constants with respect to $F_{ij}^l$.