I'm trying to train an agent on a self-written 2d env, and it just doesn't converge to the solution.
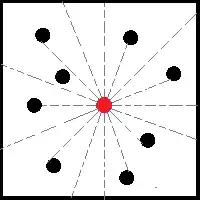
It is basically a 2d game where you have to move a small circle around the screen and try to avoid collisions with randomly moving "enemy" circles and the edge of the screen. The positions of the enemies are initialized randomly, at a minimum distance of 2 diameters from the enemy. The player circle has $n$ sensors (lasers) that measure the distance and speed of the closest object found.
The observation space is continuous and is made of concatenated distances and speeds, hence has the dimension of $\mathbb{R}^{n * 3}$.
I scale the distances by the length of the screen diagonal.
The action space is discrete (multidiscrete in my implementation) $[dx, dy] \in \{-1, 0, 1\}$
The reward is +1 for every game step made without collisions.
I use PPO implementation from Stable Baselines, but the return variance just gets bigger over the training. In addition to that, the agent hasn't run away from the enemies even once. I tried even setting the negative reward, to test if he can learn the suicide behavior, but no results either.
I thought maybe it's just possible for some degenerate policies like going to the corner of the screen and staying there to gain big returns, and that jeopardizes the training. Then I increased the number of enemies, thinking that it will enforce the agent to learn actually to avoid the enemies, but it didn't work as well.
I'm really out of ideas at this point and would appreciate some help on debugging this.