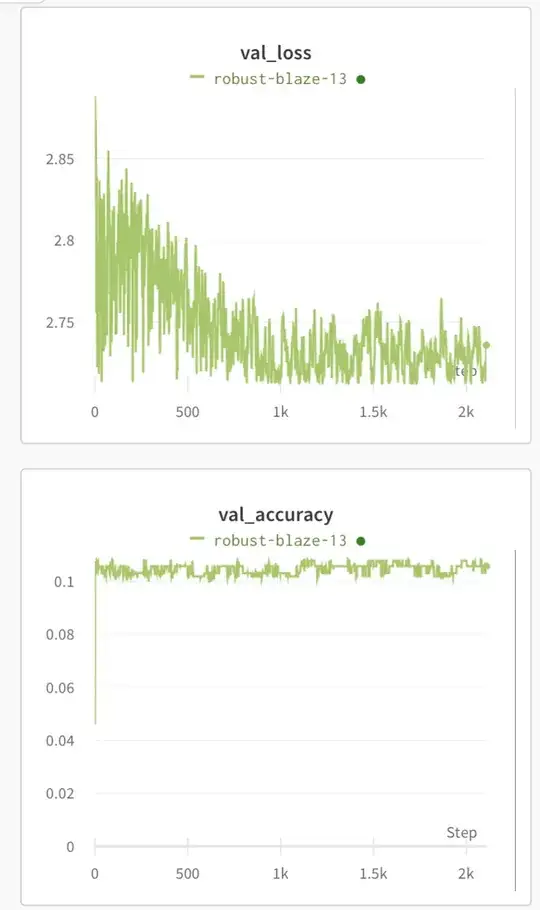
I train my neural network on random points generated for a data set that theoretically consists of approximately $1.8 * 10^{39}$ elements. I sample (generate) tens of thousands of random points on each epoch with uniform distribution. For every model I try, it appears that it cannot get past $10-12\%$ accuracy on the data, even if I increase the size of the model to over ten million parameters.
Each feature of the data set is of two Rubik's cube positions, and the corresponding label is the first move of a possible solution to solve from the first provided position to the second provided position within twenty moves.
So, it's a classification model for $18$ distinct classes, one for each of the possible moves on a Rubik's cube. Seeing that it has $12\%$ accuracy (being greater than $1/18 \approx 5.6\%$) is nice because it does mean that it is learning something, just not enough.
I also notice that loss tends to go down to a hard minimum over many epochs, but accuracy stops increasing after only around ten epochs. On epoch 36, it reached a loss of $2.713$, and it repeatedly comes back down to $2.713$, but never any lower even after 2000 epochs.
I concatenated a convolutional layer with a fully connected layer to use it as the first layer of the model. Convolutional layers might not work for this as well as I'd hope, so I throw in the fully connected layer as a safeguard. Some Keras code below:
inp_cubes = Input((2,6,3,3,1))
x = TimeDistributed(TimeDistributed(Conv2D(1024,(2,2),(1,1),activation='relu')))(inp_cubes)
output_face_conv = TimeDistributed(TimeDistributed(Flatten()))(x)
flatten_inp_cubes = TimeDistributed(TimeDistributed(Flatten()))(inp_cubes)
x = TimeDistributed(TimeDistributed(Concatenate()))((output_face_conv, flatten_inp_cubes))
x = TimeDistributed(TimeDistributed(Dense(1024,'relu')))(x)
x = TimeDistributed(TimeDistributed(Dropout(0.3)))(x)
x = TimeDistributed(TimeDistributed(Dense(1024,'relu')))(x)
x = TimeDistributed(TimeDistributed(Dropout(0.3)))(x)
x = TimeDistributed(TimeDistributed(Dense(1024,'relu')))(x)
x = TimeDistributed(TimeDistributed(Dropout(0.3)))(x)
x = TimeDistributed(TimeDistributed(Dense(1024,'relu')))(x)
x = TimeDistributed(TimeDistributed(Dropout(0.3)))(x) # face logits
x = TimeDistributed(Flatten())(x)
x = TimeDistributed(Dense(1024,'relu'))(x)
x = TimeDistributed(Dropout(0.3))(x)
x = TimeDistributed(Dense(1024,'relu'))(x)
x = TimeDistributed(Dropout(0.3))(x)
x = TimeDistributed(Dense(1024,'relu'))(x)
x = TimeDistributed(Dropout(0.3))(x) # cube logits
x = Flatten()(x)
x = Dense(1024,'relu')(x)
x = Dropout(0.3)(x)
x = Dense(1024,'relu')(x)
x = Dropout(0.3)(x)
x = Dense(1024,'relu')(x)
outp_move = Dense(18,'softmax')(x) # solution logits
I tried using only one of the two types of input layers separately, and nothing quite worked.
Loss is measured as categorical cross-entropy. I make use of time-distributed layers so that each of the two Rubik's cube positions from the input is processed equivalently, except when determining how they relate. I'm making sure to scale my data, and all that stuff. It really seems like this should just work, but it doesn't.
Is there any way to increase the model's performance without using hundreds of millions of parameters, or is that actually necessary?
I would have thought that there would be some relatively simple correlation between positions and solutions, although it's hard for us to see as humans, so maybe this comes down to the Cayley diagram of the Rubik's cube group being innately random, as though they're prime numbers or something.
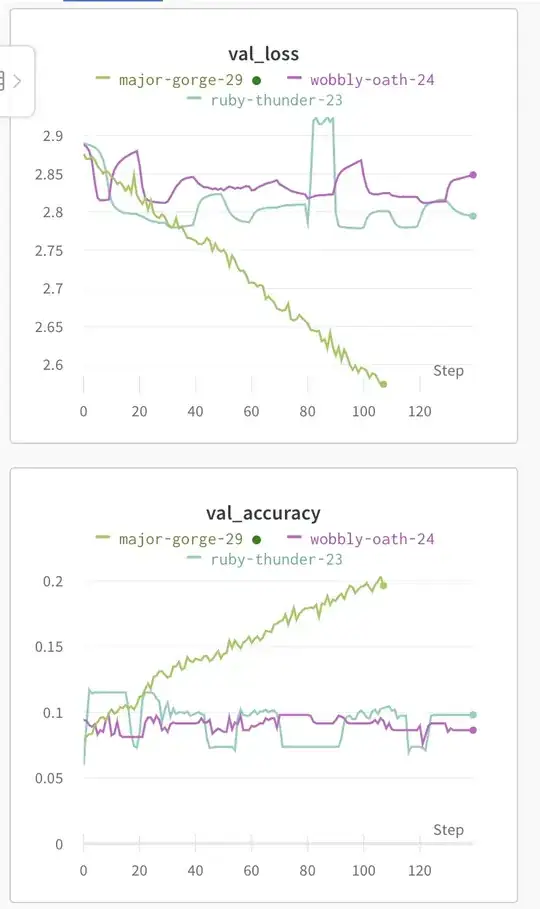
EDIT: I guess I really did just need a bigger neural network. This new on has 75 million parameters. The second image shows how that model is able to learn the data set quite easily. It takes a long time to process, though.