Why should one focus on spectral operations as a computer vision researcher?

Question

While reading about various types of mathematical operations on tensors, I encountered spectral operations for the first time.

The description is as follows (p. 53 of this book)

Spectral ops - Functions for transforming in and operating in the frequency domain, like stft and hamming_window

While going through different codes in computer vision, I have experience of using all other mathematical operations: Pointwise ops, Reduction ops, Comparison ops, and some others. But, I personally never come across any code using spectral operations on tensors.

So, I am interested in knowing whether one has an advantage in learning spectral operations in the domain of computer vision?

Answer 1

The main advantage of using spectral operations comes from the Covolution theorem, which states that the Fourier transform of the convolution of two functions is equal to the pointwise multiplication of the individual Fourier transforms of those functions.
Mathematically:

$\mathscr{F}|\it{f} \; * \it{g}| = \mathscr{F}|\,\it{f}\,| \mathscr{F}|\,\it{g}\,| $

Of course multiplying is much more convenient than convolving, and the Fourier transform is also a well known operation, and fast to compute, so that does not represent a downside.

In practice, when it comes to computer vision, the convolution theorem become fundamental for many kinds of analytic de noising and filtering methods. Instead of applying a kernel on an image on teh spatial domain using convolution, you can simply move to the frequency domain through the Fourier transform and multiplying both, image and kernel.

Moreover, when moving to the frequency domain, it become easier to access specific characteristics of images. Sharp lines and edges for example are characterized by high frequencies, so we can extract them with a simple masking operation, instead of having to came up with a tough kernel in the spatial space. This is the core idea of low and high pass filters, below here an example, where you can see that by masking the center (low frequencies) area of the spectra of two images, we can easily mix low frequency properties (e.g. shadows) and high frequency properties (e.g. edges) of two images. The same operation in the spatial domain would be tough if not impossible.

Answer 2

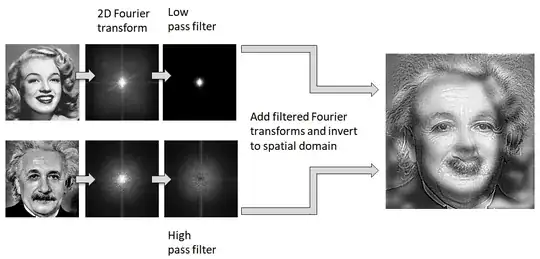
In the Fourier analysis, an image is represented by frequencies and phases. This allows to filter or transform certain frequencies or phases.

For example, Alan Oppenheim and Jae Lim have shown that phases contain information about the object contours in the image. Their paper was published in 1981, so it is poorly scanned, and the images there are not clear. Better examples are in the following books:

1. Danilo P. Mandic, Vanessa Su Lee Goh. Complex Valued Nonlinear Adaptive Filters (2009)
2. Igor Aizenberg. Complex-Valued Neural Networks with Multi-Valued Neurons (2011)

Here is an example from the second book.

Consider two images, "Lenna" and "Airplane",

Take their Fourier transform, swap magnitudes and phases of their Fourier spectra, and then perform the inverse Fourier transform. The result is as follows.

Magnitudes from the "Airplane", and phases from the "Lenna":

Magnitudes from the "Lenna", and phases from the "Airplane":

So, the information about objects is contained mainly in the phase part of the spectra.

This is what happens when amplitudes are replaced by the constant 1:

This can be used to design algorithms for image processing.

More examples of applying Fourier transform to image processing is shown in the lectures of Guillermo Sapiro where he makes really impressive things with images of HIV: part 1, part 2. That Prof.'s algorithms were used in Mars rovers.

A very good explanation of spectral techniques is given in the book, Wilhelm Burger, Mark J. Burge. Digital Image Processing. An Algorithmic Introduction Using Java (2016).