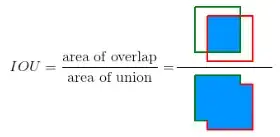
When calculating the Intersection Over Union the following explanation is widely used.
(Source: A Survey on Performance Metrics for Object-Detection Algorithms, by Padilla et al. 2020)
The image and name suggest that the denominator (the area of union) is the area of both boxes combined, box a + box b, when in reality it's not a union but rather a symmetric difference, box a + box b - intersection of box a and box b.
Why is it called "area of union" and not "area of symmetric difference"?
Consider these two sets $A = \{1, 2, 3, 4 \}$ and $B = \{0, 2, 3, 5, 6 \}$. Their union $A \cup B = \{0, 1, 2, 3, 4, 5, 6\}$. So, $|A \cup B| = 7$. The order of these numbers in $A \cup B$ does not matter, but you don't have any repeated number.
If you do $|A| + |B|$, you're effectively counting the number of elements in $A \cap B$ twice (in the example above, it would be like doing $4 + 5 = 9$, while in reality $|A \cup B| = 7$), so you subtract $|A \cap B|$ from $|A| + |B|$, i.e. $|A \cup B| = |A| + |B| - |A \cap B|$, where $|X|$ is the size of the set $X$.
See also the related Wikipedia article.
