2

So I've been tasked by my neural network professor at university to replicate the following research: Intelligent Breast Cancer Diagnosis Using Hybrid GA-ANN.

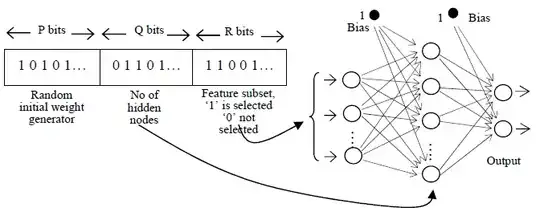
Each chromosome represents a possible net, more specifically, a possible MLP network. They've used a binary convention, and have used $P = 15$ bits for the random initial weight generator, $Q=2$ bits for the number of nodes and $R = 9$ bits for feature selection. enter image description here

P bits random initial weight generator allows 2P different combinations of the initial weight. The numbers of hidden nodes (i.e. represented by Q bits) permit the GA to explore up to a maximum of 2Q hidden nodes’ size. For the representation of the feature subset, the value of R is set to the number of full feature size. Value ‘1’ or ‘0’ indicates if the feature at that particular location is selected or otherwise.

Decode each chromosome in the population to obtain the selected feature subset, hidden node size and random generator.

I don't understand why they say with $P$ bits, there's $2*P$ combinations, wouldn't it be $2^P$? Also, I can't grasp how they decoded the $15 P$ bits into the net for the weight generation. I've searched everywhere but I can't find anything specific. What I thought to do was to transform the $15$ bits into a decimal number and use it as a specific seed for rand and randn function in Matlab, through which I make random initial weights.

JOSEPH CAROÈ
  • 21
  • 2

1 Answers1

0

I don't understand why they say with $P$ bits, there's $2*P$ combinations, wouldn't it be $2^P$?

I think you are correct here, and would suspect a typesetting issue or typo. I also think that 2Q should be $2^Q$ in the same paragraph.

Also, I can't grasp how they decoded the 15 bits into the net for the weight generation.

Without anything in the paper or associated materials, I don't think it is possible to be sure.

What I thought to do was to transform the 15 bits into a decimal number and use it as a specific seed for rand and randn function in Matlab, through which I make random initial weights.

This could work, although it will make the GA search over those 15 bits dependent on all the bits at once, due to the nature of PRNG seeds. Any crossover or mutation would destroy any coherence between generations. Perhaps that is not important, although it then does seem strange to dedicate the majority of the genome to it.

The title and description does imply that the GA is mainly being used to set start conditions for training the network, so values of P might not be very important, in which case it would mainly be used to avoid risk of poor initialisation missing the best architecture.

However, P could also be an encoded multiplier for initial randomly sampled weights, in which case the search should find stable values for the most significant digits of P. That would be similar to how Q is used (as an encoded number).

Neil Slater
  • 28,678
  • 3
  • 38
  • 60
  • Hello, thank you for your answer. I'd like to elaborate more on the solution you proposed: when you say encoded multiplier, what exactly are you suggesting? Because I already transformed the 15 bits into the actual decimal number. What should I multiply that for? Shouldn't all initial weights for both input-hidden and hidden-output layer be different? – JOSEPH CAROÈ May 19 '22 at 09:48
  • @JOSEPHCAROÈ I mean use it to multiply all randomly generated weights. You might generate weights by sampling $\mathcal{N}(0,1)$ for each one, then multiply by `P/MAX_P` – Neil Slater May 19 '22 at 13:08
  • 1
    Okay so supposedly, with P = 15, MAX_P = (2^15 - 1) and P = the decimal number of the 15 P bits. – JOSEPH CAROÈ May 19 '22 at 14:30