-1

Assuming all variables $A, B, C, D,$ and $E$ are random binary variables. I come up with Bayes net: $D \rightarrow B \rightarrow A \leftarrow C \leftarrow E$ which has the minimal number of parameters of 10, I think. However, the given choices are 8, 15, 16, 21, 23, and 32. I don't know what I did wrong?? enter image description here

BOB
  • 1
  • 2
  • I cannot understand this question. I think it is missing context, to clarify what the parameters are being used for. Could you please link or quote more from the original source? – Neil Slater May 18 '22 at 08:28
  • see the image above – BOB May 18 '22 at 08:40
  • Is this a homework problem? Is it taken from a book? If yes, which book? Can you provide more context, like, if this is a course, what course you're taking? Is this a course on Bayesian networks, statistics or something else? – nbro May 18 '22 at 08:45
  • it is a past paper from a course on ai – BOB May 18 '22 at 09:01
  • I don't really know what a Bayes Net is, or how to apply Bayes rule in this scenario, but I think the answer is (d) 21 = 1 (for A) + 4 (for B, C depending on A = 2 x 2) + 16 (for D, E, depending on A, B, C = 2 x 8). Hopefully someone can put that into terms and approach from your coursework, and I'm interested to know if I'm right. If you address nbro's questions it may help someone answer using the correct terminology. – Neil Slater May 18 '22 at 11:53

1 Answers1

0

Thanks to @Niel Slater's comment, I realized I had the wrong graph structure. The prompt is asking to first determine the graph structure given a set of conditional independencies, then second how many parameters are needed to express the joint probability distribution over five boolean variables?

1a. Given the outcome of A, the variables B and C become independent of each other.

Clearly the prompt above indicates a fork structure: $B\leftarrow A \rightarrow C$

1b. Also given A, B, and C, the variables D, and E become independent of each other.

The prompt above is slightly more difficult because I am not certain if this is saying $D\bot E | A,B,C$ or the three separate conditional independencies:

  • $D\bot E | A$
  • $D\bot E | B$
  • $D\bot E | C$

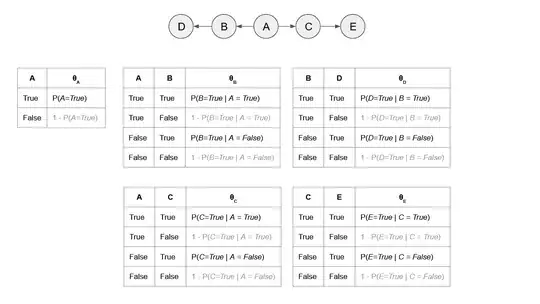
Maybe the two are the same, I am unsure, but I think the resulting graph structure assuming the latter results in the below conditional probability tables. enter image description here

There are 18 total parameters and 9 non-redundant parameters. Neither are choices. There might still be a mistake in my work, or the prompt is mistaken, or both. I will leave the original work below where I started from the wrong graph structure. I suspect I am wrong with 1b but I couldn't think of a graph structure after playing around within dagitty satisfying $D\bot E | A,B,C$ where all $A,B, C$ have to be observed at once.

Below starts with the incorrect graph structure

I don't see the correct answer among the choices from what I understand. From my interpretation of the prompt, the question asks how many parameters are needed to express the joint probability distribution over five boolean variables given the graph structure of $D\rightarrow B\rightarrow A \leftarrow C \leftarrow E$ ? If my understanding is correct, the answer should be 20, where you could use the formula $n2^k$ where $n$ is the number of boolean variables and $k$ is the maximum number of parents a node has for the given network. I can also just work out each conditional probability table for this small of a network, as shown in the picture below. 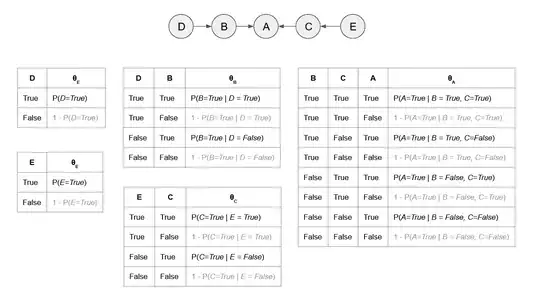enter image description here If you count up the number of rows in each table, you will get 20 parameters. Some are redundant, shown in grey, so if we only include the non-redundant parameters, we get ten parameters as the OP suggested. Without a graph structure, the number of parameters to express the full joint distribution is $2^n - 1$ resulting in 31 parameters for 32 different instantiations. There are 31 parameters since each variable only has two dimensions, with five variables ($n=5$), leaving one instantiation as redundant. If the answer is 21, I am unsure where the extra one parameter is from.

Reference

  • See page 515 of section 14.2 The Semantics of Bayesian Networks, sub section Compactness and node ordering of Artificial Intelligence: A Modern Approach Third Edition
user3587374
  • 1
  • 1