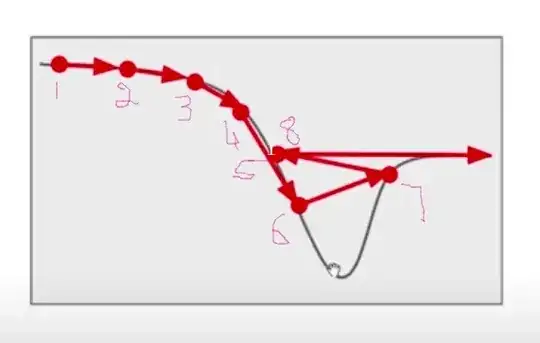
Classical gradient descent algorithms sometimes overshoot and escape minima as they depend on the gradient only. You can see such a problem during the update from point 6.
In classical GD algorithm, the update equation is
$$\theta_{t+1} = \theta_{t} - \eta \times \triangledown_{\theta} \ell$$
In the momentum based GD algorithm, the update equations are
$$v_0 = 0$$ $$v_{t+1} = \alpha v_t + \eta \times \triangledown_{\theta} \ell $$ $$\theta = \theta - \eta \times \triangledown_{\theta} \ell$$
I am writing all the equations concisely by removing the obvious variables used such as inputs to loss functions. In the lecture I'm listening to, the narrator says that momentum-based GD helps during the update at point 6 and the update will not lead to point 7 as shown in the figure and goes towards minima.
But for me, it seems that even momentum-based GD will go to point 7 and the update at point 7 will be benefited from the momentum-based GD as it does not lead to point 8 and goes towards minima.
Am I correct? If not, at which point does the momentum-based GD actually help?