Why are embeddings added, not concatenated?

Question

Let's consider the following example from BERT

I cannot understand why "the input embeddings are the sum of the token embeddings, the segmentation embeddings, and the position embeddings". The thing is, these embeddings carry different types of information, so intuitively adding them together doesn't really make sense. I mean, you cannot add 2 meters to 3 kilograms, but you can make a tuple (2 meters, 3 kilograms), so I think it's more natural to concatenate these embedding together. By adding them together, we are assuming the information about token, segmentation, and position can be simultaneously represented in the same embedding space, but that sounds like a bold claim.

Other transformers, like ViTMAE, seem to follow the trend of adding position embeddings to other "semantic" embeddings. What's the rationale behind the practice?

Answer 1

First of all, I think it is very hard to properly reason about these things, but there are a few points that might justify using sum instead of concatenation. For example, concatenation would have the drawback of increasing the dimensionality. So for subsequent residual connections to work, you would either have to use the increased dimensionality throughout the model, or add yet another layer to transform it back to the original dimensionality.

The thing is, these embeddings carry different types of information, so intuitively adding them together doesn't really make sense. I mean, you cannot add 2 meters to 3 kilograms, but you can make a tuple

I would say that because the token-embedding is learned, you cannot really compare it to a fix unit like kilogram. Instead the embedding space of the token can be optimized to work with the positional encoding under summation.

By adding them together, we are assuming the information about token, segmentation, and position can be simultaneously represented in the same embedding space, but that sounds like a bold claim.

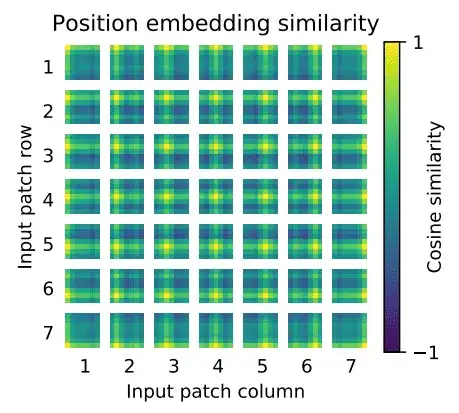
The same applies here, the problem is not to embed them into the same space, but rather that subsequent layers can separate the position information from the token information. And I think this is possible for two reasons. Firstly, if you look at the visual representation of the positional embedding, the highest distortion by summation would happen in the first dimensions:

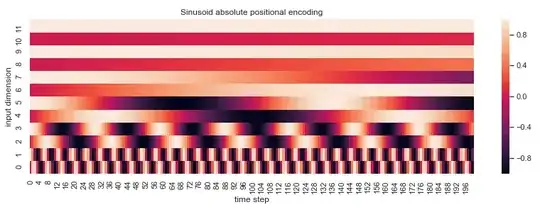(Image taken from here)

Therefore the token embedding could learn to encode high-frequency information only in the last dimensions to be less affected by the positional embedding. I think another interesting statement in the Transformer paper is that the positional encoding behaves linearly w.r.t. relative position:

We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$. [Source: Transformer Paper]

So this property shouldn't add additional non linearity to the token embedding, but instead acts more like a linear transformation, since any change in position changes the the embedding linearly. In my intuition this should also enable easy separation of positional vs token information.

This is my intuition so far, I am happy to hear your thoughts and additions

Answer 2

The confusion here is that we believe positional embedding is a more complicated version of adding positional information to the work embedding; however, it is not actually. Adding new dimensions to each embedding increases the dimensionality of the problem. On the other hand, please note that the added positional embedding is static, as shown in this image for a 2D positional embedding:

The added positional embeddings are the same for all the inputs, and the transformer can separate the positional information from the actual work embedding through the training process. Therefore, the positional embedding doesn't mess with the work embedding information, and adding them is a more efficient way of adding the positional information that concatenates them.