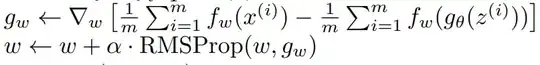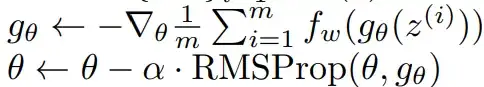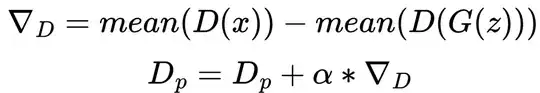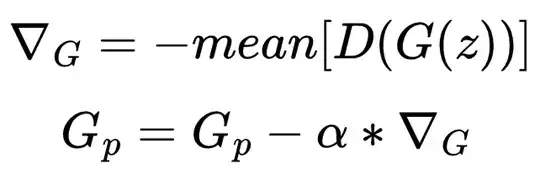What is being optimized with WGAN loss? Is the generator maximizing or minimizing the critic value?

Question

I am kind of new to the field of GANs and decided to develop a WGAN. All of the information online seems to be kind of contradicting itself. The more I read, the more I become confused, so I'm hoping y'all can clarify my misunderstanding with WGAN loss.

Critic loss function:

Generator loss function:

g_w are the parameters for the critic and g_θ are the parameters for the generator

From my understanding, the loss functions show that:

• The critic wants to minimize its loss. Splitting the loss function up, this means it wants to:
  • minimize its score on real data
  • maximize its score on fake data
• The generator wants to maximize the critic score on fake data. So it wants to make the data it generates seem more fake to the critic?

Since the critic gives a high score to fake data and a low score to real data, why would the generator want to maximize its score? Wouldn't that mean the generator wants to make its data appear more "fake" to the critic? I would think the generator would want to minimize its loss to make it look more real (since real data has a low score)

Answer 1

I think I understand what's happening with the loss functions now.

Notation:

• D = discriminator/critic
• G = generator
• D(x) - Critic score on real data
• D(G(z)) - Critic score on fake data
• ∇_D - Critic loss gradients
• D_p - Critic parameters
• ∇_G - Generator loss gradients
• G_p - Generator parameters

The loss for D essentially is as follows:

• In this case, D wants to maximize this loss (as the + indicates in the second line above). This means that D wants to make the difference as large as possible. How can it do this?
  • If D(x) is as high as possible and D(G(z)) is as low as possible, then the loss will be as high as possible.
  • D is effectively maximizing its score on real data (D(x))
  • D is also minimizing its score on fake data (D(G(z))) or maximizing its score on the flipped score on the fake data (-D(G(z)))
• So, D wants a high score for real data and a low score for fake data

The loss for G is as follows:

• In this case, G wants to minimize its loss which is -D(G(z)). This means that G wants to make the opposite of the discriminator score as low as possible. Let me break this down as it confused me a lot at first.
  • Since the loss is negative, the score is basically flipped.
  • Due to the flipped score, if D gives a positive value meaning it thinks the data is real, then the loss will be negative which G wants.
  • If D gives a negative value meaning it thinks the data is fake, then the loss will be positive which G does not want.
• Due to the double negative, this loss basically means G wants to maximize the output of the discriminator on fake data, which makes sense.

With all this in mind, I would expect the graph to look something like the following:

• D_real [maximizing D(x)] - The critic wants to produce an output that's as high as possible on real data. So, I would expect this value to be a high positive value.
• D_fake [maximizing -D(G(z))] - The critic wants to produce an output that's as low as possible on fake data. So, I would expect this value to be as high as possible. Note, I would expect D(G(z)) to be as low as possible, but due to the negative, I would expect this value to be pretty high.
• G [minimizing -D(G(z))] - The generator wants the critic to produce an output that's as high as possible. But, if you look at the loss function, you will notice the generator loss is the exact same as the discriminator loss's second term (the difference is the discriminator is maximizing its term while the generator is minimizing its term). With this in mind, I would expect the value to almost be exactly the same as D_fake (with little variation due to gradient updates).
• D - The critic wants to make its loss as high as possible, so I would expect this curve to be much higher than the rest due to it being the sum of two positive values, D_real and D_fake where D_fake is equal to G.
• So, D_fake should be fighting to make its loss higher (effectively minimizing D(G(z))) while G should be fighting to make its loss smaller (effectively maximizing D(G(z)))