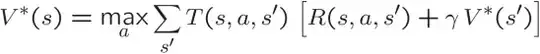Markov's Decision Process - calculate value in each iteration

Question

I have the following decision tree:

I calculated the value of the plan using the following paramenters (given): {0 → 1 , 1 → 3 , 2 → 4 }, Discount factor ()= 0.2

I used this formula to calculate the linear equations to find the value of the plan: = + ∑ ( , , )

Linear equations:

V0 = 1 + 0.2 (0.5 V0 + 0.5 V2 )

V1 = -1 + 0.2 (0.7 V0 + 0.3 V1)

V2 = -2 + 0.2 (1 V1 )

Now I need to calculate the first three iterations of the value-iteration algorithm, if a discount factor of 0.2 is used and starting initially (iteration 0) with state values all equal to 0. And write it in below format:

S0 = {Value at iteration1, value at iteration2, value at iteration3}

S1 = {Value at iteration1, value at iteration2, value at iteration3}

S2 = {Value at iteration1, value at iteration2, value at iteration3}

How can I find the value at different iterations? I know that we can use the Bellman Equation:

But how do I use this equation?

Thanks!

Answer 1

The value iteration algorithm defines the following update rule (reference is slide 11 in this MIT course): $$V_{i+1}(s) = \max_{a}\{R(s,a) + \gamma E_{s'\sim T(.|s,a)} V_i(s')\}$$ for all states $s$, with $E_{s'\sim T(.|s,a)} V_i(s') = \sum_{s'} T(s'|s,a)V_i(s')$. I adapted the transition probability name from $P$ to $T$ to conform with your notation.

Note the index $i$ for the value function on the right hand side of the equations. That's what enables you to do the computations: the value of the state at iteration $i+1$ is calculated recursively from the values at iteration $i$.

We also have $\max_a R(a,s) =$ reward for reaching the state, given that the reward assigned to each state doesn't depend on the action which was taken in your example. Therefore the value iteration update rule simplifies to: $$V_{i+1}(s) = R(s) + \gamma \max_a \{\sum_{s'} T(s'|s,a)V_i(s')\}$$

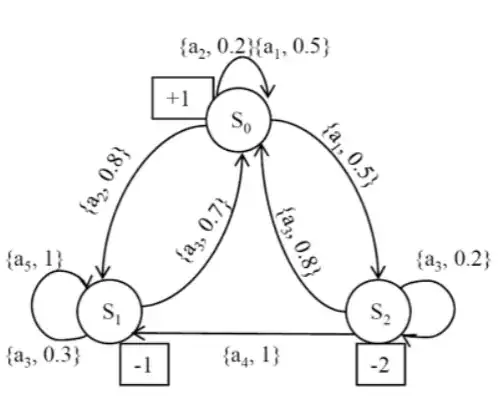
If you initialize $V_0(s)$ to the value of the reward function for that state, we have: $V_0(S_0) = 1$, $V_0(S_1) = -1$, $V_0(S_2) = -2$.

Then for $S_0$: $$\begin{align} V_1(S_0) = R(S_0) + \gamma \max \{ & T(S_0| a_1, S_0) V_0(S_0) + T(S_2 | a_1, S_0)V_0(S_2); \\ & T(S_0 | a_2, S_0) V_0(S_0) + T(S_1| a_2, S_0) V_0(S_1)\}\end{align}$$ where the first term in the $\max$ is the expected value if you take action $a_1$ from state $S_0$ and the second term is the expected value if you take action $a_2$ from state $S_0$.

This gives, with $\gamma = 0.2$ $$\begin{align}V_1(S_0) & = 1 + 0.2 * \max \{0.5*1 + 0.5 *-2; 0.2*1 + 0.8*-1\} \\ & = 1 + 0.2 * \max \{-0.5; -0.6\} \\ & = 1 - 0.2*0.5 = 0.9\end{align}$$.

Similarly for $S_1$: $$\begin{align} V_1(S_1) = R(S_1) + \gamma \max \{ & T(S_1| a_3, S_1) V_0(S_1) + T(S_0 | a_3, S_1)V_0(S_0); \\ & T(S_1 | a_5, S_1) V_0(S_1)\}\end{align}$$ which gives: $$\begin{align}V_1(S_1) & = -1 + 0.2 * \max \{0.3*-1 + 0.7*1; 1*-1\} \\ & = -1 + 0.2 * \max \{0.4; -1\} \\ & = -1 + 0.2*0.4 = -0.92\end{align}$$

And finally for $S_2$: $$\begin{align} V_1(S_2) = R(S_2) + \gamma \max \{ & T(S_2| a_3, S_2) V_0(S_2) + T(S_0 | a_3, S_2)V_0(S_0); \\ & T(S_1 | a_4, S_2) V_0(S_1)\}\end{align}$$ which gives: $$\begin{align}V_1(S_2) & = -2 + 0.2 * \max \{0.2*-2 + 0.8*1; 1*-1\} \\ & = -2 + 0.2 * \max \{0.4; -1\} \\ & = -2 + 0.2*0.4 = -1.92\end{align}$$

To get the values at the next iteration, you can reuse the equations above incrementing the indices by one.