Bayesian optimization with confidence bound not working

Question

I have a simple MLP for which I want to optimize some hyperparameters. I have fixed the number of hidden layers (for unrelated reasons) to be 3. So the hyperparameters being optimized through Bayesian Optimization are just number of neurons per hidden layer.

Here is the function to create the simple MLP based on number of neurons in each of the 3 hidden layers:

#function for creating a new MLP with number of neurons in 3 layers for argument 
def creat_model(layer1, layer2, layer3):
  input = tf.keras.layers.Input(shape = (28,28))
  x = tf.keras.layers.Flatten()(input)
  x = tf.keras.layers.Dense(layer1, activation = 'relu')(x)
  x = tf.keras.layers.Dense(layer2, activation = 'relu')(x)
  x = tf.keras.layers.Dense(layer3, activation = 'relu')(x)
  output = tf.keras.layers.Dense(10, activation = 'softmax')(x)
  model = tf.keras.models.Model(inputs = input, outputs = output)
  model.summary()
  model.compile(loss = 'sparse_categorical_crossentropy', optimizer = 'adam')
  return model

Then I define the search space:

#creating the search space
layer_range = np.arange(1,128,16)
all_ranges = []
for i in layer_range:
  for j in layer_range:
    for k in layer_range:
      all_ranges.append([i, j, k])

The following vectors are to store all losses and their corresponding parameters:

#vector of all losses
loss_vec = []
#vector of all params
all_params = []

The GP model is created like this:

model_gp = GaussianProcessRegressor()

note the default kernel is RBF.

Then I randomly sample from this search space and fit the model to these sampled points:

num_of_rands = 5
for i in range(num_of_rands):
  rand_layer = all_ranges[np.random.randint(len(all_ranges))]
  layer1 = rand_layer[0]
  layer2 = rand_layer[1]
  layer3 = rand_layer[2]
  all_params.append([layer1, layer2, layer3])
  model = creat_model(layer1, layer2, layer3)
  model.fit(x_train, y_train, batch_size = 64, epochs = 2)
  lossPoint = model.evaluate(x_test, y_test)
  loss_vec.append(lossPoint)

model_gp.fit(all_params, loss_vec)

Then, using the simple lower confidence bound approach, I run this loop to find the best set of parameters:

#bayes opt loop
runs = #insert number of runs
lmbda = 1
for i in range(runs):
  y_hat, std = model_gp.predict(all_ranges, return_std=True)
  ix = np.argmin(y_hat - lmbda*std)
  new_sample = all_ranges[ix]
  model = creat_model(new_sample[0], new_sample[1], new_sample[2])
  model.fit(x_train, y_train, batch_size = 64, epochs = 2)
  lossPoint = model.evaluate(x_test, y_test)
  loss_vec.append(lossPoint)
  all_params.append(new_sample)
  model_gp.fit(all_params, loss_vec)

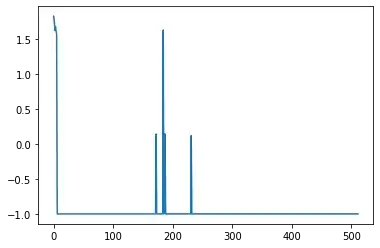
Now the problem is, the model starts from [1,1,1], then to [1,1,17], and so on! to explore this further, I plotted the prediction of the GP across the parameters and it looked sth like this (this is mean - lambda*standard deviation):

Note x-axis indices are just different sets of params, e.g. [1,1,1], [1,1,17], [1,1,33], ... As seen, there is no smoothness, and the model starts to sample every single point, you can see the random sampled points somewhere in the middle and the ones sampled through the loop near 0... why is this? what's the fix? I usually see this GP approach to produce smooth predictions, not here though!