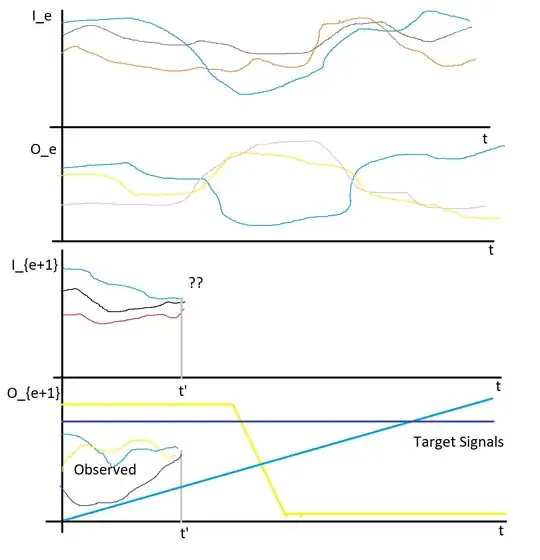
Assume I've run a set of initial experiments. For each experiment, I have a set of input signals $I_e(i, t)$, and output signals $O_e(j, t)$ for $i \approx 10$, $j \approx 10$, and $0\leq t\leq t_{max}=7200$ for half-second timesteps. This gets me a set of experiments $1 \leq e \leq N$. So $O_e = F(I_e)$ for some function $F$.
I have a target signal to match the desired output signals for a given $T(i, t)$ by controlling the $j$ input signals on the fly for a new experiment but only have the data for the run for the start to the present time, e.g. $O_{e+1}(i, t')$ with $ 0 \leq t' < t_{max}$. I'd like to do this iteratively, so hopefully each succeeding experiment would be more accurate. This would also need to be run in real-time.
Which ML approach should I use? It seems like reinforcement learning/q-learning would be the right approach? I'm not sure how that would work with partial time data as a state.
