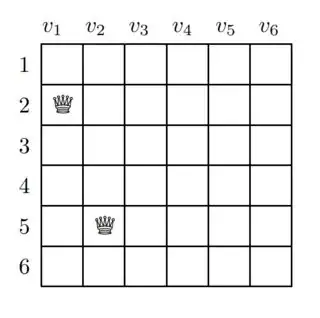
Consider the following board:
The exercise asks to apply the AC-3 algorithm, given that the domain of $v_1$ and $v_2$ is fix with $v_1 = 2$ and $v_2 = 5$. For the remaining domains, we should initially consider the whole domain $v_3 = v_4 = v_5 = v_6 = \{1,2,3,4,5,6\}$. The constraints are, that no value should be affected vertically, horizontally or diagonally by any other value. First, I want to explain how I tackled the problem:
Starting with the variable $v_3$, we can see that the values $\{2,4,5,6\}$ are not arc consistent with either $v_1$ or $v_2$, hence after the first iteration we have an updated domain of $v_1 = \{1,3\}$ and would add each constrain affecting $v_3$ back to the queue.
Moving on to $v_4$, we see that $\{2,3,5\}$ conflict with either $v_1$, $v_2$ or $v_3$, and thus we have an update domain $v_4 = \{1,4,6\}$. Again, we add each constrain affecting $v_4$ back to the queue.
Moving to $v_5$, we see that only $\{4\}$ is valid. We have removed values from that domain, so we add every constraint back to the queue.
At this point, I would consider $v_6$ and just repeat the procedure, however, the solution considers $v_4$ again, and I cannot possible see why.
Am I doing something wrong with the queue? Even if it was a FIFO queue, that the solution considered, I expect $v_3$ to be checked again before $v_4$.
I will also upload the solution for reference: