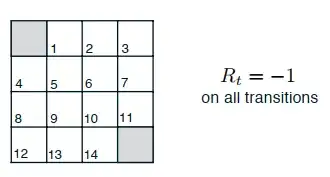
Consider the simple environment below, where the gray cells are the terminal states and the agent receives a reward of $-5$ for taking any action in these states. The nonterminal states are $S = \{1, 2, . . . , 14\}$. There are four actions possible in each state, $A = \{up, down, right, left\}$, which deterministically cause the corresponding state transitions, except that actions that would take the agent off the grid in fact leave the state unchanged.
My question is which value of $R_t \in \{-5, -0.5, 0, 5\}$ will yield a policy that returns the shortest path to the terminal state? Let's assume the agent starts from cell $12$.
The discount factor is assumed to be γ=0.9.