What would be a good optimization technique for this kind of problem?

Question

Problem Description:

Since I am not sure if there is a scientific term that categorizes this problem, I will do my best to describe it thoroughly. Suppose there is a chamber that's being filled with poisonous gas. The amount of poisonous gas being released at 1-second intervals can be represented as a time series such as:

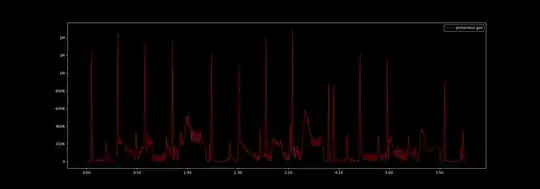
In order to reduce the poisonous gas, the operator has access to a set of jobs, which if initiated at a certain time, can release a certain amount of neutralizing gas per second over a certain duration. Specifically, a job can be represented as $$J_i(amount_i, duration_i, cooldown_i)$$ where:

• $amount_i$ is the amount of neutralizing gas released by $J_i$ per second
• $duration_i$ is how long $J_i$ lasts when activated
• $cooldown_i$ is how long $J_i$ is unavailable before it can be used again. Note that this property is what makes this optimization problem difficult (more on that later).

Note that in this particular problem, at any timestamp $t$, the neutralizing gas can only reduce the poisonous gas that is present at timestamp $t$. So in other words, it doesn't linger.

$Problem_1$: If the operator has access to a set of jobs $J = ({J_0, J_1, J_2, ...})$, what would be the best placements of jobs in order to end up with the least total amount of poisonous gas remaining in the chamber?

There are many possible solutions, but a good one would have to allocate a job with the right amount at the right time. Because remember if a high-throughput job is allocated when there is hardly any poisonous gas being released, then it would all go to waste. The cooldowns are also a big factor since the assignments would have consequences on the entire timeline. Hence, I reckoned this might be a good optimization candidate for AI.

An example of a solution can be shown as:

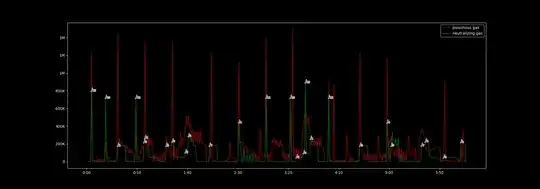
What makes this problem difficult is the cooldown constraint for every job. Because the constraint is not on the range of values, but rather on the different possible solutions. What I mean is that if the optimization algorithm comes up with a potential solution that uses $J_0$ at timestamp $t$, it somehow needs to understand that it should ignore any other solution that tries to use $J_0$ between timestamps $t$ and $t + cooldown_0$. I assume the optimization algorithm that is useful for the problem should be somehow capable of that.

Question:

What would be a good optimization technique to solve (or approximate) $Problem_1$ given its jobs' cooldown constraint?

More info (what I have tried):

• PSO: I was hoping to use Particle Swarm Optimization, but the issues are:

  • High number of dimensions: To be able to map job assignments to particles, the number of dimensions blows up to number of jobs * total_duration_seconds. So for example for 15 different jobs over 6 minutes, it would result in 5400 particle dimensions, where each dimension can be either 0 or 1. So for example, if particle_dimensions[3] is 1 then it represents using the 1st job ($J_0$) at timestamp = 4 seconds. Similarly if particle_dimensions[360 + 5] is 1, then it represents using the 2nd job ($J_1$) at timestamp = 6 seconds. Is there a better way of mapping the particles so that the number of dimensions are lower?
  • Job cooldown: more importantly, the cooldown constraint makes the search space full of unfeasible areas which makes finding feasible solutions very difficult. Because if $J_0$ is used at 4 seconds, represented by $particle\_dimensions[3] = 1$ then only at index $particle\_dimensions[3 + cooldown_0]$ and later the value can be 1 again. All the values in between must be 0, otherwise, it would violate the cooldown constraint for $J_0$. Now imagine this must be held true for all jobs, so the whole 5400 dimensions need to be set in a way that none of them violate the cooldowns of each job respectively. In order to tackle this, I have assigned a penalty to unfeasible solutions, but they are so many that the particles cannot find their way into the few (very spread-apart) feasible areas. Is this why using PSO is a bad idea here? Or is there a way to tell particles how they should move in order to respect the cooldown constraint for each and every job? Is that even possible?

• Constrained Programming: I am not very familiar with this paradigm, but it seems interesting given the cooldown constraint. Do you think this would be a good approach to tackle the cooldown constraint?