0

In Convolutional Neural Networks we extract and create abstractified “feature maps” of our given image. My thought was this: We extract things like lines initially. Then from different types of lines we are meant to extract higher order features. However, doesn't this require us to look at multiple feature maps at once? Convolutional layers only apply the filter on one matrix at a time, and the only time, to my knowledge, that these feature maps get looked at together is at the fully connected layer.

To explain further, if we have an image of a circle we want to recognize, this consists of many lines at different angles. But in a convolutional layer, we have these different filters that will pick up different parts of the circle. Then when we add a second convolutional layer, how can it extract a higher order feature without combining feature maps in some way? Do we combine feature maps in between convolutional layers?

Brian Przezdziecki
  • 3
  • 1

2 Answers2

0

I'm not quite sure what you mean by "combining" these maps, but here is a simple example (in Keras):

model = keras.models.Sequential([
    layers.InputLayer((res, res, 1)),
    layers.Conv2D(3, 7, activation='sigmoid'),
    layers.Conv2D(3, 7, activation='sigmoid'),
    
    layers.GlobalMaxPooling2D(),
    layers.Dense(1, activation='sigmoid')
])

Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_199 (Conv2D)          (None, 42, 42, 3)         150       
_________________________________________________________________
conv2d_200 (Conv2D)          (None, 36, 36, 3)         444       
_________________________________________________________________
global_max_pooling2d_92 (Glo (None, 3)                 0         
_________________________________________________________________
dense_102 (Dense)            (None, 1)                 4         
=================================================================
Total params: 598
Trainable params: 598
Non-trainable params: 0

I used sigmoid activations on the convolutional layers as well (with three "kernels"), since their outputs are easy to visualize as RGB images.

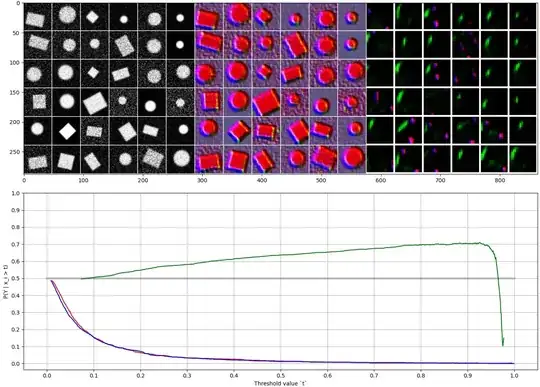
I trained the network on generated 48x48 grayscale images, each showing either an ellipse or a rectangle. Input images are shown on the top right, and they are normalized so that 25% of the pixels are black and 2% are white.

The intermediate output is quite hard to interpret, but the second output (before global max pooling) correlates well with the input images, and also with the output target class. The green channel seems to correspond to circles and ellipses (detecting curvature?), while red and blue channels react to linear lines. These correlations are also shown in the lower plot.

Then when we add a second convolutional layer, how can it extract a higher order feature without combining feature maps in some way?

Note that while the first Conv2D layer has weights of shape [7, 7, 1, 3] (ignoring the bias), the seconds one has a shape of [7, 7, 3, 3]. Eg. it sees all three channels of the previous layer simultaneously, meaning three "separate" matrices. So "convolutional layers only apply the filter on one matrix at a time" isn't quite true. Instead they apply to one tensor at a time, which can be interpreted as stacked matrices.

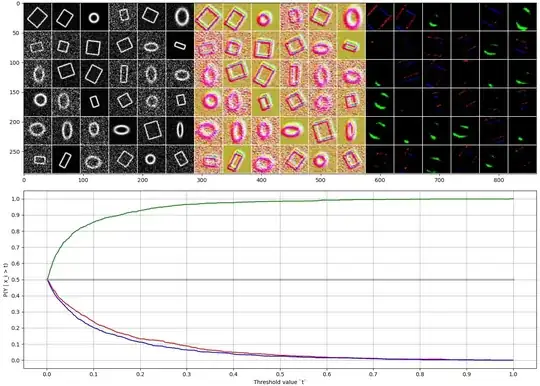
network outputs 1

Note that the network may learn to detect very different aspects, depending on the initial parameters and specifics of the data. For example in this case the shapes are filled solid, and the network makes the distinction whether there are corners in the image or not. The green channel alone doesn't seem to be good for this classification task.

network outputs 2

NikoNyrh
  • 642
  • 4
  • 8
  • Thanks so much this definitely cleared up my confusion! "So "convolutional layers only apply the filter on one matrix at a time" isn't quite true. Instead they apply to one tensor at a time, which can be interpreted as stacked matrices." Okay, I see the filter/kernel can also be a tensor. Interesting. So would the order of your feature maps matter? It would seem to me that they would then. In this case where there is 3 channels it wouldn't, but if the kernel was smaller, the order of the feature maps would make some difference right? – Brian Przezdziecki Nov 22 '22 at 11:37
  • Wait actually, no it doesn't. Because the kernels before are learned. Okay sorry if I'm being confusing, don't worry about it I got it now! – Brian Przezdziecki Nov 22 '22 at 11:38
  • Ah, a simpler way to put this is to think of a color image with RGB color channels. The first convolution kernel looks at all of the color channel simultaneously, while seeing just a certain part of the image (depending on the kernel's width and height). And usually the number of channels increases as we add more layers to the network, but the math is still the same. A RGB image can be thought of as three matrices, or a single tensor. – NikoNyrh Nov 22 '22 at 19:30
0

Also I would suggest you to have a look at the term "Receptive field" in CNNs(Which actually look at scaled version of what the previous Conv layer looked at while it did a convolving step. Reference is - https://towardsdatascience.com/intuitively-understanding-convolutions-for-deep-learning-1f6f42faee1.

So Inherently it is looking at what the previous layer looked at for that particular filter all through the input image's overall area

Udemmy Udemmy
  • 1