What does the figure in Q-learning vs Expected SARSA actually show?

Question

I might be blind. But I wasn't able to find or figure out what the small difference between Q-learn and SARSA depicts in the following image; 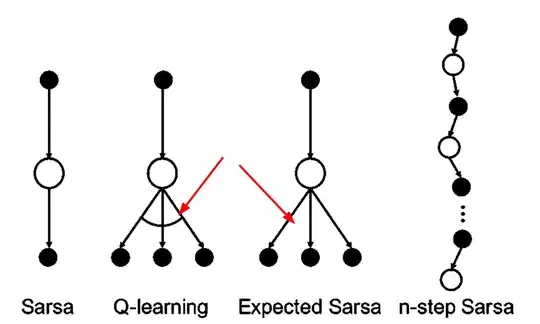(src). What does the semi-circle show? and what does the lack of the semi-circle show? I've your eyes with some red arrows.

Answer 1

It is a reference to the difference between their update rules.

While both are attempting to estimate $Q(S_t,A_t)$ by iterative updates, the formula they use to converge on this value is different.

Expected SARSA uses a weighted sum over the latest estimations of $Q(s_{t+1}, a)$ for all actions in the new state (weights are the probability assigned to taking that action by the policy):

$$ Q(S_t,A_t) \leftarrow (1-\alpha)\cdot Q(S_t,A_t) + \alpha \cdot\left[R_{t+1} + \gamma\sum_a\pi(a | S_{t+1})Q(S_{t+1}, a)\right] $$

Q-Learning uses the maximum expected value over all actions in the new state:

$$ Q(S_t,A_t) \leftarrow (1-\alpha)\cdot Q(S_t,A_t) + \alpha \cdot\left[R_{t+1} + \gamma\max_aQ(S_{t+1}, a)\right] $$

So, to answer directly: the semi-circle represents taking the maximum.