Suppose we've got the following formula:
$\log p(x;\theta)=\mathbb{E}_{q(z|x;\phi)}[\log p(x,z;\theta)-\log q(z|x;\phi)]+KL(q(z|x;\phi)||p(z|x;\theta))\\ \geq \mathbb{E}_{q(z|x;\phi)}[\log p(x,z;\theta)-\log q(z|x;\phi)]$
We call this Evidence Lower Bound (ELBO):
$\mathrm{ELBO}=\mathbb{E}_{q(z|x;\phi)}[\log p(x,z;\theta)-\log q(z|x;\phi)]$
We use the method of maximizing ELBO to optimize the parameters $\theta$ and $\phi$:
$\max_{\theta,\phi}\mathbb{E}_{\mathcal{D}}\mathbb{E_{q(z|x;\phi)}}[\log p(x,z;\theta)-\log q(z|x;\phi)]$
We can intuitively understand that: for given $\theta$, the upper bound of ELBO is $\log p(x;\theta)$, so optimizing $\phi$ allows ELBO to be as close as $\log p(x;\theta)$ possible; Then, optimizing $\theta$ can make the data likelihood as large as possible, which achieves the goal of MLE. (just like what shown in Fig)
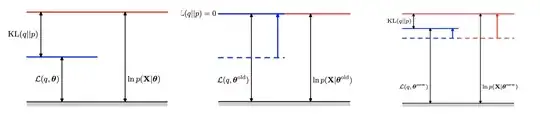
The ELBO mentioned above is also the loss function of VAE. (An algebraic transformation of the ELBO mentioned above: $\mathrm{ELBO}=\mathbb{E}_{q(z|x;\phi)}[\log p(x|z;\theta)]-KL(q(z|x;\phi)||p(z;\theta))\\\\$)
My question is:
1.When maximizing ELBO, how can I fix $\theta$ and then $\phi$, as mentioned above?
2.VAE optimizes them at the same time, there is no precedence. How could I understand the difference?