0

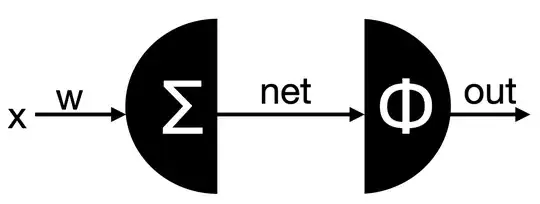
Assuming a single perceptron (see figure), I have found two versions of how to use backpropagation to update the weights. The perceptron is split in two, so we see the weighted sum on the left (the output of this is net) and then the sigmoid function phi on the right (the output of this is out).

enter image description here

So for the backpropagation portion, we compute $\frac{\delta cost}{\delta w}=\frac{\delta cost}{\delta out}\times \frac{\delta out}{\delta net} \times \frac{\delta net}{\delta w}​$, to find how the weight affects the error.

For the portion $\frac{\delta out}{\delta net}$ I have seen three different versions for how to compute the value:

  1. $\frac{\delta out}{\delta net}$ = $\phi'(out) = \phi(out) \times (1 - \phi(out))$
  2. $\frac{\delta out}{\delta net}$ = $\phi'(net)= \phi(net) \times (1 - \phi(net))$
  3. $\frac{\delta out}{\delta net}$ = $out \times (1 - out)$

Can somebody explain to me which one is correct and why? Or is there one which should be preferred?

Robin van Hoorn
  • 1,810
  • 7
  • 32
HTH
  • 1
  • 1
    Could you provide sources for the three different versions you have seen? – Robin van Hoorn Jan 20 '23 at 15:41
  • For 1. https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/, for 2. https://towardsdatascience.com/how-to-build-your-own-neural-network-from-scratch-in-python-68998a08e4f6 and for 3. https://ai.stackexchange.com/questions/5638/are-my-computations-of-the-forward-and-backward-pass-of-a-neural-network-with-on – HTH Jan 22 '23 at 12:34
  • Please clarify your specific problem or provide additional details to highlight exactly what you need. As it's currently written, it's hard to tell exactly what you're asking. – Community Jan 25 '23 at 19:48
  • If I'm understanding you, you have some input "x" and the output "out", but it's not clear to me what equations you are using to go from x to out. Are those the \sigma and \phi functions? – Taw Jan 25 '23 at 19:49

1 Answers1

1

  1. is always wrong. Most implementations then "silently" correct this error, even if the docstrings have this wrong variant, in the actual use it is done correctly.

  2. and 3. are the same, considering that $out=\phi(net)$. 3. is more economic if the activation is a solution of an autonomous ODE like with the logistic function. 2. is more generally true, especially if the activation function gets modified/perturbed by some linear function to avoid random behavior in the flat parts of the sigmoid at large values.

Lutz Lehmann
  • 206
  • 1
  • 5