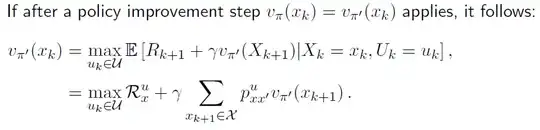Policy iteration means to improve the policy step by step, so that $v_{\pi}(x_{k}) \leq v_{\pi'}(x_{k})$ for all $x \in X$. If we have $v_{\pi}(x_{k}) = v_{\pi'}(x_{k})$ for all $x \in X$, this means that we do not need to iterate the policy any further since the resulting actions of $\pi$ and $\pi'$ are of the same quality and so we have already found the optimal policy. As you mentioned
\begin{equation}
\pi'(x_{k}) = \underset{u_{k}\in U}{\mathrm{argmax}}~q_{\pi}(x_{k}, u_{k})
\end{equation}
and also, since we are using a greedy policy (s. Sutton-Barto eq. 3.18 for the last equality sign and this answer for a step-to-step derivation)
\begin{equation}
v_{\pi'}(x_{k}) = v_{\pi}(x_{k}) = \max_{u_{k}\in U} q_{\pi}(x_{k}, u_{k}).
\end{equation}
From here it follows
\begin{align}
v_{\pi'}(x_{k}) = \max_{u_{k}\in U} q_{\pi}(x_{k}, u_{k}) =\max_{u_{k}} \mathbb{E} [R_{k+1} + \gamma v_{\pi}(X_{k+1})|X_{k} =x_{k}, U_{k}=u_{k}]
\end{align}
and since the equality $v_{\pi}(x_{k}) = v_{\pi'}(x_{k})$ for all $x_{k} \in X$ we can do the final step:
\begin{align}
v_{\pi'}(x_{k}) = \max_{u_{k}\in U} q_{\pi}(x_{k}, u_{k}) =\max_{u_{k}} \mathbb{E} [R_{k+1} + \gamma v_{\pi'}(X_{k+1})|X_{k} =x_{k}, U_{k}=u_{k}]
\end{align}
Edit: This is the answer I posted to an older version of the question, where it was not clear that OP wanted to know how to derive the first line, but I rather assumed that the simplification between line one and two was asked to explain.
The second line in your equation is actually just the matrix notation (s. slide 9 in your document) of the first one and shows how to build the expectation value.
\begin{align}
v_{\pi'}(x_{k}) &= \max\limits_{u_{k} \in U} \mathbb{E} [R_{k+1} + \gamma v_{\pi'}(X_{k+1})|X_{k}=x_{k}, U_{k}=u_{k}] \\
&= \max\limits_{u_{k}} R^{u}_{x} + \gamma \mathbb{E} [v_{\pi'}(X_{k+1})|X_{k}=x_{k}, U_{k}=u_{k}] \\
&= \max\limits_{u_{k}} R^{u}_{x} + \gamma \sum_{x_{k+1} \in X}p(x_{k+1} | x_{k}, u_{k}) v_{\pi'}(x_{k+1}) \\
&=\max\limits_{u_{k}} R^{u}_{x} + \gamma \sum_{x_{k+1} \in X}p^{u}_{xx'} v_{\pi'}(x_{k+1})
\end{align}
In the first step, we just build build the expectation value over the reward and moved $\gamma$ out of the expectation value. Then Just build the expecatation value, so calculate the value function of a given state $x_{k+1}$ with the probability of ending up there. Then finally, just change the notation to fit with the standard notation provided by OP.