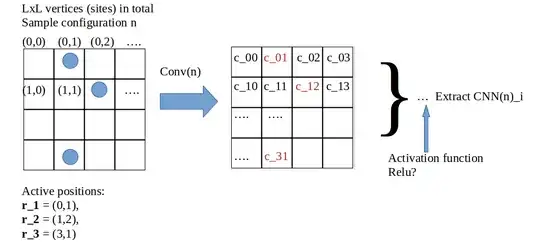
Let us suppose we have a squared grid and some particles (active vertices) that are distributed on it. We can construct a 2D image, where basically the input image is a matrix with 0s (no particle) and 1s (particle present). This corresponds to a sampled configuration $n$.
I need to calculate some terms $f(n)_i$ that takes as input all the positions/configuration $n$ and are associated to the particle $i$. An important conditions is that it needs to respect translation equivariance.
My first attempt is to use a Convolutional layer CNN:
My questions are:
1.) How to interpret the output image Conv(n)? Are these probability distributions that represent the occupation probability of the particles on site $i$ ?
2.) Are CNN expressive enough that I can simply extract the $f(n)_i = CNN(n)_i$ from the output image Conv(n) or do I need to add another layer, e.g. a max pooling layer where I will extract the maximal values (in total extract 3 values for 3 particles).