2

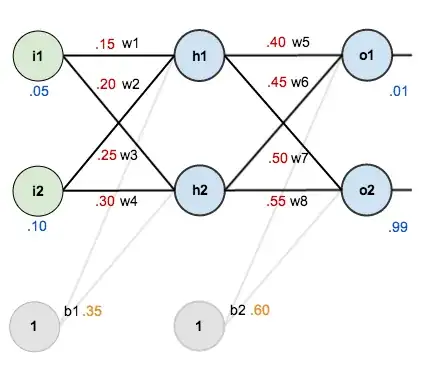
Suppose we have the following neural network (in reality it is a CNN with 60k parameters): Neural network

This image, as well as the terminology used here, is borrowed from Matt Mazur

As is visible, there are two neurons in the output layer, namely o1 and o2. However, I do not have labels for these neurons. Rather, I have another neural network that evaluates this output layer and return one value that indicates the "goodness". As such, it is impossible to calculate the individual errors for o1 and o2, but it is possible to use aforementioned goodness as total error (i.e., the sum of the errors for o1 and o2). Thus, as I see it, every term in the following chain-rule formula can still be calculated:

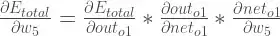Chain rule formula (And a similar formula for o2.)

Is my understanding as described above correct? And, if yes, would this be implemented in Keras simply as follows?

def custom_loss(y_true, y_pred):
    return loss_model(y_pred)

main_model.compile(optimizer="adam", loss=custom_loss)
Value_Investor
  • 23
  • 3
  • 1
    If you use a NN to evaluate the total error from above output layer with two units, then you equivalently morph the original post's vector function (mapping from $R^2$ to $R^2$) approximation problem into fitting the usual nonlinear regression problem (from $R^2$ to $R$). If this is the case, why not just add a transfer function in the last layer of the above original NN which could guarantee to produce similar result per the universal function approximation theorem? – mohottnad Feb 13 '23 at 20:39

0 Answers0