For $t=0,1,\dots$, consider a parameter $x_t \in ${$1, \dots, n$}, where $n \in \mathbb{N}$, and a shape $S(x_t)$ on an $m \times m$ square grid $G$. Let's denote the status of a cell $(i,j) \in G$ at time $t$ by $s_t(i,j) \in \{0,1\}$. We mark the shape on the grid at time $t$ using the status of all cells $(i,j) \in G$ as $s_t(i,j) = 1$ if $(i,j) \in S(x_t)$ and $s_t(i,j) = 0$ if $(i,j) \not\in S(x_t)$. I have illustrated this in image 1.
1: 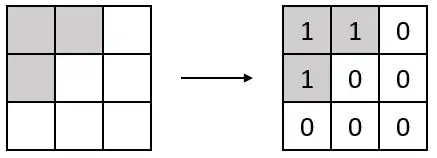
Consider that at each time $t$, the parameter $x_t$ takes values randomly (or using an update equation from $x_{t-1}$ to $x_t$) from $x \in$ {$1,\dots, n$}. Then, we receive a one-hot encoded observation $o_t$ which is consistent with the current shape $S(x_t)$, i.e., the cell which takes a value of $1$ in $o_t$ is a cell which also takes a value of $1$ in $S(x_t)$. I have illustrated the feasible observations for a given shape in image 2.
2: 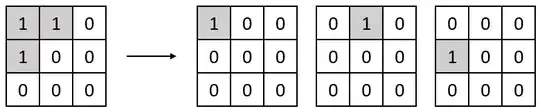
Goal: I want to train a neural network using the sequence of data $(x_t, o_t)$ for $t=0, 1, \dots$ to learn a stationary mapping from each parameter $x \in$ {$1, \dots, n$} to the corresponding shape $S(x)$.
So far, I have trained a neural network to learn such a mapping from each parameter to its corresponding shape "offline," as follows: I pre-processed the observation data to merge the observations corresponding to each parameter $x \in$ {$1, \dots, n$} so that effectively I am training with the knowledge of the entire shape at each time $t$ using the data point $(x_t, S(x_t))$. In this case, I used a differentiable approximation of the Hausdorff metric and dice loss to define the loss function of my neural network. This is an idea from image segmentation: Reducing the Hausdorff Distance in Medical Image Segmentation with Convolutional Neural Networks.
However, I am confused about how I can achieve this task in an "online" setting, where I want to learn the mapping from parameters to shapes using only sampled observation data. Let's denote the neural network's predicted shape at any time $t$ for a parameter $x \in$ {$1, \dots, N$} by $S^p_t(x)$. Note that the predicted shape $S^p_t(x)$ is likely a "soft" shape, i.e., each cell $(i,j)$ of the grid $G$ has a continuous predicted status $s^p_t(i,j) \in [0,1]$.
So far, I have the following ideas to achieve this task:
Consider a window of $N \in \mathbb{N}$ time steps starting at some time $\bar{t}$ with a data sequence $((x_{\bar{t}}, o_{\bar{t}}), \dots, x_{\bar{t} + N}, o_{\bar{t} + N}) )$. For all $t = \bar{t}, \dots, \bar{t}+N$, we fix the neural network's output to a shape $S^p_{\bar{t}}(x_t)$. Then, we use a similar approximation of the Hausdorff distance $d_H(\cdot, \cdot)$ directly on the observations and average it across time, to get the loss $\dfrac{\sum_{t = \bar{t}}^{\bar{t}+N} d_H \big(S^p_\bar{t}(x_t), o_t \big)}N$. Then, backpropagate to train the neural network once with respect to this loss, move on to time $t=N+1$ and repeat this process.
Consider the same approach as the first idea but with an approximate Chamfer distance $d_C(\cdot, \cdot)$ to define the loss function instead of the approximate Hausdorff distance. Here, we would have to approximate the Chamfer distance to work with the soft prediction of the neural network and I am as of yet unsure about how to do this.
Consider an RNN, like an LSTM, instead of a regular neural network in either the first or second ideas. This may allow the neural network to track a representation of "history of observations" and learn to better predict the underlying set from observation data.
Request: I would really appreciate any and all help towards figuring out how to achieve this goal!
Are there any standard techniques or approaches to such problems that I am missing?
I do not have a complete background in such problems and am still learning. For example, I know that a KL Divergence based loss can be used to learn a probability distribution from sampled points. Is there a similar idea that I can use to learn a shape or set from sampled points?
Are there other ways to look at this problem which make it easier to solve?
Thank you for taking the time to read my very long question and many thoughts!