Are there any toy classification problems that can't be solved with logistic regression, but can be solved with a NN with exactly one hidden node?

Question

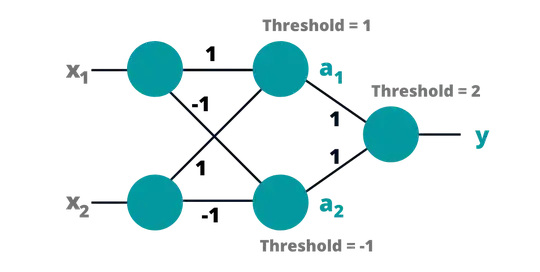
Basically, I'm wondering if there are any small and simple problems that are:

• complex enough to be unsolvable with a standard neural network without any hidden layer (ie. input -> output)
• simple enough to be solvable with a standard neural network consisting on exactly one hidden node in exactly one hidden layer (ie. input -> one hidden node -> output)

Can such problems even exist at all? If not, why?

Answer 1

With one hidden node, there is one single input to the output neuron.

Therefore, the two neurons are equivalent to a single neuron with activation function the composition of the two activation functions.

This collapses the two layers into one, so no problem can be solved with only one single hidden neuron that is not solved with no hidden layer.

Answer 2

With exactly one hidden neuron, I believe the answer is no. The hidden neuron has one input and one output, and thus all it does is scale the final output by its activation function. Thus, it does not accomplish anything.

However, with a very slight tweak, the answer is yes. If we instead consider a network with exactly 2 hidden neurons, this becomes a very famous problem.

The XOR problem cannot be solved without a hidden layer, but is solvable with one hidden layer consisting of 2 neurons.

Famously, this limitation of single layer perceptrons led Marvin Minsky to be very critical of research on Neural Networks in the 1970s, and was a contributor to the first AI winter.

Here is an example of an XOR, which could not be computed with no hidden layer: