Introduction
I am considering to use a convolutional neural network in implementing Monte Carlo control with function approximation. I am using a Monte Carlo estimate as it is unbiased and has nice convergence properties. Of course, it has high variance and slower convergence.
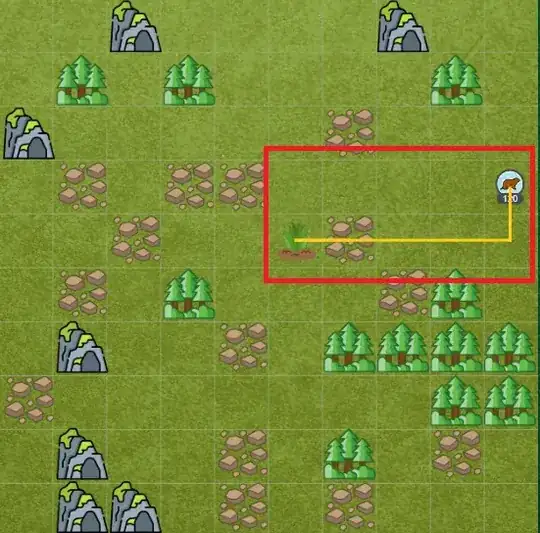
The goal is to control a game such that episodic reinforcement learning is used. In fact, the game is Mckinsey Plant-defense game. Below is an image of the game:
Problem specification
I have written a rough simulator of the game and then written a function that splits the board into various 14 x 14 layers. More specifically, the layers contain the following:
- Layer 1 is a
(14,14)array of zeros with a 1 at the location of the plant. - Layers 2-4 are
(14,14)arrays of zeros with ones placed at coordinates containing terrain. For example, layer 2 contains only the location of cliffs. - Layers 5-7 are like layers 2-4 but contain locations of defenders, i.e., snake.
- Layers 8 and 9 are also
(14,14)arrays of zeros. However, if an attacker is present at $(i,j)$ in the grid, a value between zero and 1 is placed there. A such, both the remaining health and location are presented in a layer. Layer 8is for the foxes and layer 9 is for the groundhogs. - The grid of the actual game varies. Sometimes it's a
(10,10)grid,(14,10),(12,12), etc. As such, I cast these grids onto a(14,14)grid. The last layer is thus a(14,14)array of zeros with ones placed in locations that do not exist. In other words, the ones indicate where I have padded the original grid. For example, a(12,12)grid would have a border of ones.
Naturally, there is spatial interaction in each layer but also interaction between layers. I am considering two approaches to a convolution architecture. Note, I am using PyTorch, so I apologise if I am using PyTorch-specific terminology.
Approaches: 2D (with channels) vs 3D (no channels) convolution
Approach 1
Approach 1 uses 2D convolution with channels.
$$
y_{h,i,j} = \sum_{k=1}^{C_{in}}\sum_{l=1}^{H_k}\sum_{m=1}^{W_k}w_{h,k,l,m}x_{k,i+l-1,j+m-1}
$$
Where $h=1,2,\dots,C_{out}$ are output channels, $k=1,2,\dots,C_{in}$ is the input channels, $l=1,2,\dots,K_H$ is the height of the kernel, $m=1,2,\dots,K_W$ is the width of the kernel, $x$ is the layers of the map and $y$ is the output of the convolution. In PyTorch's Conv2d function, if I set groups=1 then all input channels are convolved with all output channels as in the formula. Does this capture interaction between channels?
Approach 2
The second approach would instead treat the 10 stacked layers as a 3D image of shape (10,14,14) with one channel. The formula for this would read as below:
$$ y_{i,j,k} = \sum_{m=1}^{D_k}\sum_{n=1}^{H_k}\sum_{o=1}^{W_k}w_{m,n,o}x_{i+m-1,j+n-1,k+o-1} $$ It would seem that this would capture more of the dependencies between layers? I would imagine that this is the approach they would use in medical imaging where the image has layers that strongly interact.
Question
Which approach is most suitable for modelling dependencies within layers and between layers? Can you please provide me with some intuition on why? I would also not mind reading recommended literature. Thank you for your time.