How do we get the optimal value-function?

Question

In here it says that: (is it correct?)

$$V^\pi = \sum_{a \in A}\pi(a|s)*Q^\pi(s,a)$$

And we have:

$$ V^*(s) = max_\pi V^\pi(s)$$

Also:

$$ V^*(s) = max_a Q^*(s, a) $$

Can someone demonstrate to me step by step how we got from $ V^*(s) = max_\pi V^\pi(s)$ to $ V^*(s) = max_a Q^*(s, a) $ ?

And is it correct that $ V^\pi(s) = max_{a \in A} Q^\pi(s,a) $ ?

Answer 1

Bellman Expectation Equations

Let's first look at the definition of the value functions.

The state-value function $V^\pi(s_t)$ is defined as the expected return $G_t=\sum_{t'=t} \gamma^{t-t'} r_{t'}$ we get from state $s_t$, and then following the policy $\pi$ until termination: $$\begin{align} V^\pi(s_t) &= \mathbb{E}_\pi\big[r_t + \gamma r_{t+1} + \gamma^2 r_{t+2}+\cdots\mid s_t\big] \\ &= \mathbb{E}_\pi\big[G_t\mid s_t\big] \\ &= \mathbb{E}_\pi\big[r_t + \gamma G_{t+1}\mid s_t] \\ &= \mathbb{E}_\pi\big[r_t + \gamma V^\pi(s_{t+1})\mid s_t] \end{align}$$

• Basically, we get a recursive equation in which $V^\pi(s_t)$, at the current time $t$, is defined as the immediate reward $r_t=r(s_t,a_t)$ plus the discounted state-value of the next timestep $t+1$.

Now, the definition of the action-value function, $Q^\pi(s_t,a_t)$ is similar in that we start from state $s$, but take action $a$, and then follow $\pi$: $$\begin{align} Q^\pi(s_t,a_t) &= \mathbb{E}_\pi\big[G_t\mid s_t,a_t\big] \\ &= \mathbb{E}_\pi\big[r_t + \gamma Q^\pi(s_{t+1}, a_{t+1})\mid s_t,a_t] \\ \end{align}$$

Turns out that these two value functions are related, in the sense that one can be written in terms of the other: such relationship is depicted by the backup diagrams.

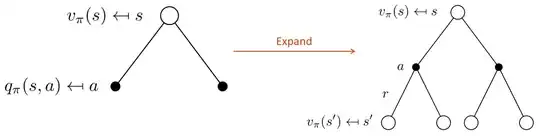
• For the $V$-function, the root of the backup tree is a state $s$ whose leaves are all the possible actions $a\in A$.
• When computing $V^\pi(s)$ we need to consider all the leaves, i.e. the action-values. This is done by averaging their values and weighting by the probability of that action to occur (thus computing an expectation), which is provided by the policy. So, the diagram on the left provides a first relationship: $$\begin{align} V^\pi(s) &=\mathbb{E}_\pi\big[Q^\pi(s,a)\big]\\ &= \sum_{a\in A}\pi(a\mid s) Q^\pi(s,a) \end{align}$$
• If we further expand the diagram (right) by executing a given action in the env, we experience a reward $r$, landing in a new state $s'\in S$. But we still need to reason in "expectation", this time starting from an action node. Stating that the Q-value can be written in terms of the state-value as follows: $$\begin{align} Q^\pi(s,a) &=r(s,a) + \gamma\sum_{s'\in S}p(s'\mid s,a) V^\pi(s') \end{align}$$
• where $p(s'\mid s, a)$ is the probability (determined by the environment) of transitioning to next state $s'$ by tacking action $a$ in the current state $s$.

A similar diagrams exists for $Q$, except that we start from an action. Now we can substitute the new equations to compute both $V$ and $Q$ functions: $$\begin{align} V^\pi(s) &= \sum_{a\in A}\pi(a\mid s)\Big(r(s,a) + \gamma\sum_{s'\in S} p(s'\mid s,a) V^\pi(s') \Big)\\ Q^\pi(s,a) &=r(s,a) + \gamma\sum_{s'\in S}p(s'\mid s,a) \sum_{a'\in A}\pi(a'\mid s') Q^\pi(s',a') \end{align}$$

The last two equations allow to estimate both value functions in terms of them selves, instead the previous ones in terms of each other. Being able to compute such functions allow to evaluate the goodness of a policy $\pi$, know also as policy evaluation.

Bellman Optimality Equations

The expectation equations can be modified to obtain the optimal value functions: the key idea is to take the $\max$ instead of the expectations. In general we have: $$\begin{align} V^\star(s) &= \max_\pi V^\pi(s) \\ Q^\star(s,a) &= \max_\pi Q^\pi(s,a) \end{align}$$

Considering the previous relationships between $V$ and $Q$, we can write: $$\begin{align} V^\star(s) &= \max_\pi V^\pi(s) \\ &= \max_a Q^\star(s,a) \\ &= \max_a r(s,a) + \gamma \sum_{s'\in S}p(s'\mid s,a) V^\star(s') \end{align}$$

In a similar way is possible to rewrite $Q^\star$ too. In general these formulas are explained by the following backup diagrams:

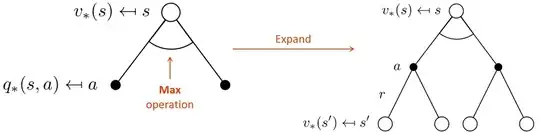
• This is the optimal backup diagram for $V^\star$, a similar one exists for $Q^\star$.
• Notice that the $\max$ is only taken over actions (that replaces $\sum_{a\in A}\pi(a\mid s)$ in the expectation eq.), and not over states. For the states we still consider an expectation but computed accordingly to the transition probability, i.e. $\sum_{s'\in S}p(s'\mid s, a)$.

Is it correct that $V^\pi(s)=\max_{a\in A}Q^\pi(s,a)$?

If you're doing policy evaluation no. Because $V^\pi(s)$ is the value averaged over actions, not the maximum which is useful for policy improvement instead: i.e. to derive the best action that the policy should take in $s$, which turns out to improve the current policy and so $V^\pi$ since it's an action that exploits.

Reference: David Silver's RL course.

Answer 2

There's no way to prove in general for any policy $\pi$ you always have $ V^\pi(s) = \max_{a \in A} Q^\pi(s,a) $ since there's no $\max$ operator on the left hand side and semantically there could exist averaging relationship over actions between them if your $\pi$ is a stochastic policy, but not $\max$ relationship.

For you main concern, here's the steps from your definition of $V^*(s), Q^*(s)$ and define optimal policy $$\pi^* = \arg \max_\pi (\sum_{a\in A}\pi(a | s) Q^\pi(s,a)) $$, then we have: $$\begin{align} V^*(s) &= \max_\pi V^\pi(s) \\ &= \max_\pi (\sum_{a\in A}\pi(a | s) Q^\pi(s,a)) \\ &= \sum_{a\in A}\pi^*(a | s) Q^{\pi^*}(s,a) \end{align}$$

In case an optimal policy $\pi^*$ is deterministic, we have $\pi^*(a | s) = \begin{cases} 1, a=a^*(s) \\ 0, a \neq a^*(s) \end{cases}$, where $$a^*(s)=\arg \max_a Q^{\pi^*}(s,a)$$, thus we further have: $$\begin{align} V^*(s) &= Q^{\pi^*}(s,a^*) \\ &= \max_{a \in A} Q^{\pi^*}(s,a) \end{align}$$

Finally note if $\pi^*$ is deterministic, $$Q^{\pi^*}(s,a)=\max_\pi Q^\pi (s,a)=Q^*(s,a)$$, so you arrive at $$V^*(s) = \max_{a \in A} Q^*(s,a) $$