2

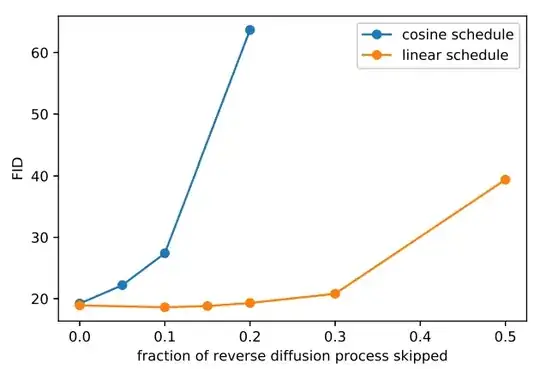
Could you provide the explanation of Figure 4 from the paper at Improved Denoising Diffusion Probabilistic Models?

(1) The paper says, "the end of the forward noising process is too noisy,and so doesn’t contribute very much to sample quality". But if the goal is to have an image with only noise, why is it problematic to have a lot of noise?

(2) The paper says, "a model trained with the linear schedule does not get much worse (as measured by FID) when we skip up to 20% of the reverse diffusion process". But why is it the reverse diffusion process? Shouldn't the deterioration be related to the forward process?

(3) Also, why is the training process relevant?

It seems to me that the explanation of this section means 'linear noise schedule is better than cosine one'. Could you explain, please?

enter image description here

diffusion stable
  • 41
  • 6

2 Answers2

1

I will suppose that you already have understood how diffusion models work. Some good resources are this blog and the DDPM paper.

If we look at Figure 3 of the paper, we see that in linear schedule the image are almost purely noise in the last quarter. During sampling, we usually perform the same number of steps the model was trained on, but in the linear schedule the reverse process will just turn some random noise into some other random noise for 1/4 of the time.

Linear vs cosine schedule comparison

  1. If those steps are irrelevant in terms of image quality (estimated using FID), it means that we are just wasting time (and a bunch precious energy to run GPUs)
  2. They are measuring the quality of generated images by the diffusion model. The generative direction is in the reverse process. The authors observed that the quality of images generated during sampling does not change much if the denoising step is skipped a few times. This means that instead of performing the whole 4K denoising steps, we can do less without losing performance
  3. Another proposed solution of this paper is in the learned variances $\Sigma_\theta(x,t)$. The original paper sets $\Sigma_\theta(x,t)= \sigma^2 I$, while this paper proposes an interpolation $$\Sigma_\theta(x,t)= \exp(v \log \beta_t + (1-v) \log \tilde{\beta_t})$$ In figure 8 they show that with this modification the number of sampling steps can be reduced without losing image quality (measured by FID). All but $\Sigma_\theta(x,t)= \beta^2 I$ obtain the same performance in 400 vs 4K denoising steps.
Ciodar
  • 242
  • 8
  • Thank you for reply. I understand about the Figure 8. On the other hand , does Figure 4 mean that the cosine schedule gets much worse when skipped up to 20%? – diffusion stable Jul 08 '23 at 01:15
  • In the case of Figure 4, does it mean cosine schedule is not good? – diffusion stable Jul 08 '23 at 01:22
  • @diffusionstable no, the cosine schedule is good because intuitively every denoising step is useful to produce a better image, whereas in linear schedule many steps do not contribute in improving the final result. – Ciodar Jul 08 '23 at 06:43
1

Intuitively, the noise schedule shall be smooth and progressive enough to be easily approximated by the NN. In this context, a linear schedule is plausibly too "easy", and hence prone to overfitting.

In contrast, the modulation of the cosine schedule provides a slightly more challenging task to the NN (yet remaining smooth and gradual), so that when the reverse process is learnt, it is more robust.

Peblo
  • 11
  • 3