7

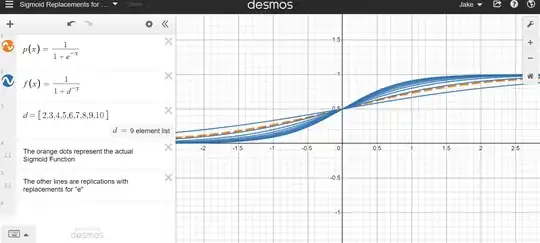
Within the Sigmoid Squishification function,

f(x) = 1/(1 + e^(-x))

"e" is unnecessary, as it can be replaced by any other value that is not 0 or 1. Why is "e" used here?

As shown below, the function is working well without that, and in replacement, any other number that's greater than 1. All of them

  • Squish the number between 0 and 1
  • Reach (0, 0.5)
  • Make an "S" curve
  • Has a working derivative
  • Have similar derivatives, with Maximas varying on the replacement of Euler's number

The function and derivative with "d" as the parameter replacement can be written as:

const sigmoid = (x, d) => 1/(1 + d**(-x));
const sigmoid_derivative = (x, d) => (d**x) * Math.log(d) / ((d**(x)) + 1)**2;

https://www.desmos.com/calculator/xpkhdijt3v

enter image description here

Jake
  • 81
  • 4
  • 4
    Using $e^{-x}$ is a writing convention, what you really use is the standard library function $\exp(-x)$. The implementation of $\exp(x)$ is optimized, with guaranteed error rate. The power function for $d^x$ is composite of other primitive library functions, with much overhead to guarantee similar error rates. – Lutz Lehmann Aug 14 '23 at 06:20
  • 3
    Remember that $a^x=e^{x log a}$. So yeah, they are all the same, its just easier to work with $e$ – Ander Biguri Aug 14 '23 at 14:48
  • The point of using the sigmoid with $e$ is that you can simply calculate the derivative using the equation $f'(x) = f(x)(1 - f(x))$. Using a built-in method to calculate the derivative defeats the purpose of using the sigmoid function, which is that it has a derivative with a simple algebraic form in terms of $f$. – Charles Hudgins Aug 15 '23 at 02:47

4 Answers4

18

The choice of $e$ is convenient when taking derivatives.

Compare $\frac{d}{dx} \exp(x)$ to $\frac{d}{dx} a^x$ for any other $a > 0$.

Sycorax
  • 453
  • 5
  • 12
5

If $d$ is a positive real number different from $1$, then

$$d^{-x}=e^{-x\ln(d)}$$

So $d^{-x}$ is obtained from $e^{-x}$ by a horizontal shrink (when $\ln(d)>1$, that is $d>e$) or by a horizontal stretch (when $\ln(d)<1$, that is $0<d<e$).

The general shape of the graph is the same but it is raising faster from (close to) $0$ to (close to) $1$ when $d$ is large.

The choice of $e$ is convenient as the derivative of $e^x$ is slightly simpler than $d^x$ (as explained by @Sycorax), making it the default choice in the mathematical literature.

Taladris
  • 151
  • 1
  • 2
    Worth noting that the horizontal scaling is learnable by the network by scaling the weights. So no generalisation is lost. – Neil Slater Aug 14 '23 at 06:30
5

To add to other answers: Note that the usefulness of $e$ as the base is not limited to this particular case of sigmoid activation function. It is the go-to base in so many areas of mathematics because of many nice properties (including the reasons given in other answers); see e.g. the exponential function in Wikipedia.

In fact, the choice is so natural (pun intended) that if any other base was chosen, people would ask the question "$d$ is unnecessary, why not just use $e$ as the base?"

JiK
  • 151
  • 2
2

$f$ is the unique function such that $f(0) = \frac{1}{2}$ and $f'(x) = f(x)(1 - f(x))$. Using $e$ is necessary to make sure the derivative takes this very simple form.

Charles Hudgins
  • 121
  • 1
  • This combines with binary cross entropy loss, to make a simple combined gradient with respect to the logits in logistic regression and binary classifiers. – Neil Slater Aug 15 '23 at 15:47