Background
Generative modeling
Generative modeling aims to model the probability of observing an observation x.
$$
p(x) = \frac{p(y\cap x)}{p(y|x)}
$$
Representation Learning
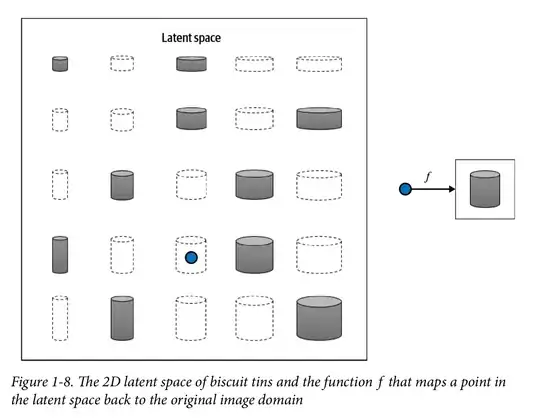
Instead of trying to model the high-dimensional sample space directly, we describe each observation in the training set using some lower-dimensional latent space and then learn a mapping function that can take a point in the latent space and map it to a point in the original domain
Context:
Let’s suppose we have a training set consisting of grayscale images of biscuit tins
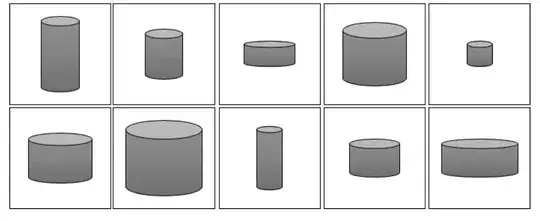
we can convert each image of a tin to a point in a latent space of just two dimensions. We would first need to establish two latent space dimensions that best describe this dataset(height, width), then learn the mapping function f that can take a point in this space and map it to a grayscale biscuit tin image.
Question:
What is:
P(y|x): is it possibility of point lying in Latent space given it is a point in (high dimensional) pixel space?
Or for that matter, what do x, y, P(x), P(y), P(x|y) really mean/represent here?
P.S.: this is referred from the book Generative Deep Learning 2nd edition By David Foster, O'Reilly Publication.