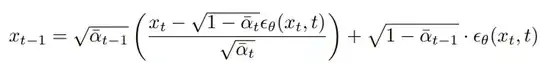Background & Definitions
In DDPM, the diffusion backward step is described as follows (where $z\sim \mathcal{N}(0,I)$ and $x_{T}\sim \mathcal{N}(0,I)$):
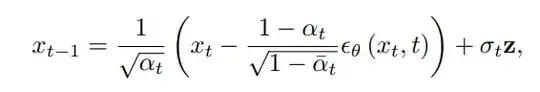
and in DDIM we have
while in the SDE formulation (from the Fokker-Planck equation) the step is:
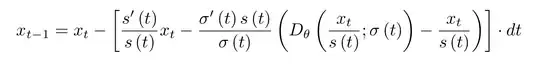where $D_\theta$ is the denoiser network trying to predict $x_0$ (We can also instead predict the noise $\epsilon_\theta$ using the relation $x_t = x_0 + \sigma(t)\cdot\epsilon$), and $s,\sigma$ are the functions defining the diffusion forward process: $x_t \sim \mathcal{N}(s(t)\cdot x_0, s(t)\sigma(t)I)$.
The Question
I was wondering if the SDE formulation is actually a "generalized" version of DDPM. Meaning, can we find $s,\sigma$ s.t. the two processes are the same. (meaning, the discretization of SDE can result in DDIM/DDPM).
My hypothesis is that they are, and since in DDPM/DDIM I believe the forward process is described by $$\begin{array}{c} x_{t}\sim\mathcal{N}\left(\sqrt{\bar{\alpha}_{t}}x_{0},\left(1-\bar{\alpha}_{t}\right)I\right)\\ \alpha_{t}:=1-\beta_{t}\\ \bar{\alpha}_{t}=\prod\limits _{k=1}^{t}\alpha_{k} \end{array}$$
and in the SDE formulation it is described by $$x_t \sim \mathcal{N}(s(t)\cdot x_0, s(t)\sigma(t)I)$$ an appropriate choice seems to be $$\begin{array}{c} s\left(t\right)=\sqrt{\bar{\alpha}_{t}}\\ \sigma\left(t\right)=\frac{1-\bar{\alpha}}{\sqrt{\bar{\alpha}_{t}}} \end{array}$$
but of course this is not defined for all $t$ values since SDE is continuous and DDPM/DDIM are discrete. I am unable to prove that the backwards processes are indeed the same. Perhaps a different choice of $s,\sigma$ is needed? or perhaps they can't be shown to be equivalent/need additional components.
