What is the difference between encoders and auto-encoders?

Question

How are the layers in a encoder connected across the network for normal encoders and auto-encoders? In general, what is the difference between encoders and auto-encoders?

Answer 1

Theory

Encoder

• In general, an Encoder is a mapping $f : X \rightarrow Y $ with $X$ Input Space and $Y$ Code Space
• In case of Neural Networks, it is a Generative Model hence a function which is able to compute a Representation out of some input (like GAN)

The point is: how would you train such an encoder network ?

• The general answer is: it depends on what you want your code to be and ultimately depends on what kind of problem the NN has to solve, so let's pick one

Signal Compression

The goal is to learn a compressed representation for your input that allows to reconstruct the original input minimizing the loss of information

In this case hence you want the dimensionality of $Y$ to be lower than the dimensionality $X$ which in the NN case means the code space will be represented by less neurons than the input space

Autoencoder

Focusing on the Signal Compression problem, what we want to build is a system which is able to

• take a given signal with size N bytes

• compress it into another signal with size M<N bytes

• reconstruct the original signal, starting from the compressed representation, as good as possible

To be able to achiebve this goal, we need basically 2 components

• an Encoder which compresses its input, performing the $f : X \rightarrow Y$ mapping

• a Decoder which decompresses its input, performing the $f: Y \rightarrow X$ mapping

We can approach this problem with the Neural Network Framework, defining an Encoder NN and a Decoder NN and training them

It is important to observe this kind of problem can be effectively approached with the convenient learning strategy of unsupervised learning : there is no need to spend any human work (expensive) to build a supervision signal as the original input can be used for this purpose

This means we have to build a NN which operates essentially between 2 spaces

• the $X$ Input Space

• the $Y$ Latent or Compressed Space

The general idea behind the training is to make a certain input go along the encoder + decoder pipeline and then compare the reconstruction result with the original input with some kind of loss function

To define this idea a bit more formally

• The final autoencoder mapping is $f : X \rightarrow Y \rightarrow X$ with
  • the $x$ input
  • the $y$ encoded input or latent representation of the input
  • the $\hat x$ reconstructed input
• Eventually you will get an architecture similar to

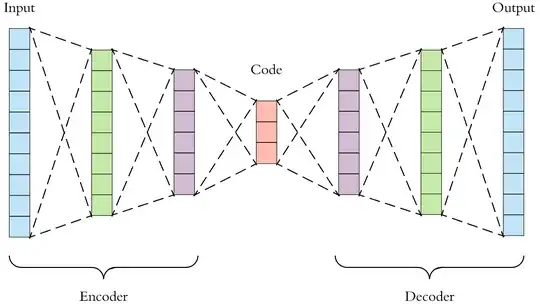
• You can train this architecture in an unsupervised way, using a loss function like $f : X \times X \rightarrow \mathbb{R}$ so that $f(x, \hat x)$ is the loss associated to the $\hat x$ reconstruction compared with the $x$ input which is also the ideal result

Code

Now let's add a simple example in Keras related to the MNIST Dataset

from keras.layers import Input, Dense 
from keras.models import Model 

# Defines spaces sizes 

## MNIST 28x28 Input 
space_in_size = 28*28

## Latent Space 
space_compressed_size = 32 

# Defines the Input Tensor 
in_img = Input(shape=(space_in_size,))

encoder = Dense(space_compressed_size, activation='relu')(in_img)

decoder = Dense(space_in_size, activation='sigmoid')(encoder)

autoencoder = Model(in_img, decoder)

autoencoder.compile(optimizer='adam', loss='binary_crossentropy')

Answer 2

As an addition to NicolaBernini's answer. Here is a full listing which should work with a Python 3 installation that includes Tensorflow:

"""MNIST autoencoder"""

from tensorflow.python.keras.layers import  Input, Dense, Flatten, Reshape
from tensorflow.python.keras.models import Model 
keras.datasets import mnist
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure

"""## Load the MNIST dataset"""

(x_train, y_train), (x_test, y_test) = mnist.load_data()

"""## Define the autoencoder model"""

## MNIST 28x28 Input 
image_shape = (28,28)

## Latent Space 
space_compressed_size = 25 

in_img = Input(shape=image_shape)
img = Flatten()(in_img)
encoder = Dense(space_compressed_size, activation='elu')(img)
decoder = Dense(28*28, activation='elu')(encoder)
reshaped = Reshape(image_shape)(decoder)
autoencoder = Model(in_img, reshaped)
autoencoder.compile(optimizer='adam', loss='mean_squared_error')

"""## Train the autoencoder"""

history = autoencoder.fit(x_train, x_train, epochs=10, shuffle=True, validation_data=(x_test, x_test))

"""## Plot the training curves"""

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.legend(['loss', 'val_loss'])
plt.show()

"""## Generate some output images given some input images. This will allow us to see the quality of the reconstruction for the current value of ```space_compressed_size```"""

rebuilt_images = autoencoder.predict([x_test[0:10]])

"""## Plot the reconstructed images and compare them to the originals"""


figure(num=None, figsize=(8, 32), dpi=80, facecolor='w', edgecolor='k')
plot_ref = 0

for i in range(len(rebuilt_images)):

  plot_ref += 1
  plt.subplot(len(rebuilt_images), 3, plot_ref)
  
  if i==0:
    plt.title("Reconstruction")
  
  plt.imshow(rebuilt_images[i].reshape((28,28)), cmap="gray")
  
  plot_ref += 1
  plt.subplot(len(rebuilt_images), 3, plot_ref)
  
  if i==0:
    plt.title("Original")
  
  plt.imshow(x_test[i].reshape((28,28)), cmap="gray")
  
  plot_ref += 1
  plt.subplot(len(rebuilt_images), 3, plot_ref)
  
  if i==0:
    plt.title("Error")

  plt.imshow(abs(rebuilt_images[i] - x_test[i]).reshape((28,28)), cmap="gray")

plt.show(block=True)

I have changed the loss function of the training optimiser to "mean_squared_error" to capture the grayscale output of the images. Change the value of space_compressed_size to see how that effects the quality of the image reconstructions.

Answer 3

To answer this rather succinctly, an encoder is a function mapping some input to some different space. An example of this is what the brain does. We have to process the sensory input that the environment gives us in order for it to be storable.

An autoencoder's job, on the other hand, is to learn a representation(encoding). An autoencoder will have the same number of output nodes as there are inputs for the purposes of reconstructing the inputs instead of trying to predict the Y target. Autoencoders are usually used in reducing output dimensions in high dimensional data sets.

Hope I answered your question!