How to compute the derivative of the error with respect to the input of a convolutional layer when the stride is bigger than 1?

Question

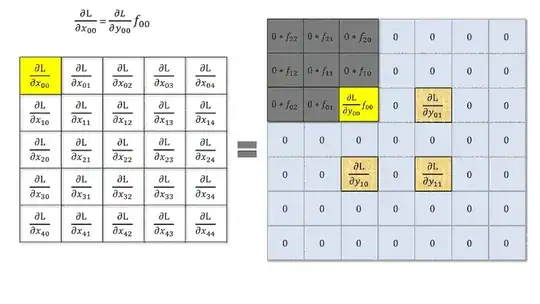
I read that to compute the derivative of the error with respect to the input of a convolution layer is the same to make of a convolution between deltas of the next layer and the weight matrix rotated by $180°$, i.e. something like

$$\delta^l_{ij}=\delta^{l+1}_{ij} * rot180(W^{l+1})f'(x^l_{ij})$$

with $*$ convolution operator. This is valid with $stride=1$.

However, what happens when stride is greater than $1$? Is it still a convolution with a kernel rotation or I can't make this simplification?

score 3 · Answer 1 · answered May 07 '19 at 21:06

3

Backpropagation with stride > 1 involves dilation of the gradient tensor with stride-1 zeroes. I created a blog post that describes this in greater detail.

answered May 07 '19 at 21:06

Mayank

131
3

score 1 · Answer 2 · answered Apr 02 '18 at 14:47

1

From the paper found from the post linked below:

'We find that max-pooling can simply be replaced by a convolutional layer with increased stride without loss in accuracy on several image recognition benchmarks'

All that means that only values are skipped (=pooling is made) to the matrix, otherwise all works like a convolution should do.

Sources:

https://arxiv.org/pdf/1412.6806.pdf

https://stackoverflow.com/questions/44666390/max-pool-layer-vs-convolution-with-stride-performance

answered Apr 02 '18 at 14:47

mico

927
1
8
16

This is not an answer to my question; you are talking about pooling, my question is about simple convolution in backpropagation algorithm. – volperossa Apr 02 '18 at 14:52
Well, the point is that strides introduce pooling kind of phenomenom and otherwise it does not change CNN performance and if I read my source right, also correctness. – mico Apr 02 '18 at 14:55
Probably more direct professional expertice you could get on datascience.SE site. I belong to both of these, thus I knew sth of the issue. – mico Apr 02 '18 at 15:01

score 1 · Answer 3 · edited Dec 30 '21 at 13:38

I have just the same problem, and I was trying to derive the backpropagation for the convolutional layer with stride, but it doesn't work.

When you do the striding in the forward propagation, you chose the elements next to each other to convolve with the kernel, then take a step $>1$. This results in the fact that in the backpropagation, in the reverse operation, the delta matrix elements will be multiplied by the kernel elements, (with the rotation) but not as strided, but you are picking elements that are not next to each other, something like $DY_{11} * K_{11} + DY_{13} * K_{12} + DY_{31} * K_{21} + DY_{33} * K_{22}$, which is NOT the equivalent as a convolution with a stride $>1$.

So as far as I am concerned, if I would like to implement the ConvNet by myself to get a better grasp of the concept, I have to implement a different method for the backprop, if I allow strides.

How to compute the derivative of the error with respect to the input of a convolutional layer when the stride is bigger than 1?

3 Answers3