In a nutshell: I want to understand why a one hidden layer neural network converges to a good minimum more reliably when a larger number of hidden neurons is used. Below a more detailed explanation of my experiment:
I am working on a simple 2D XOR-like classification example to understand the effects of neural network initialization better. Here's a visualisation of the data and the desired decision boundary:
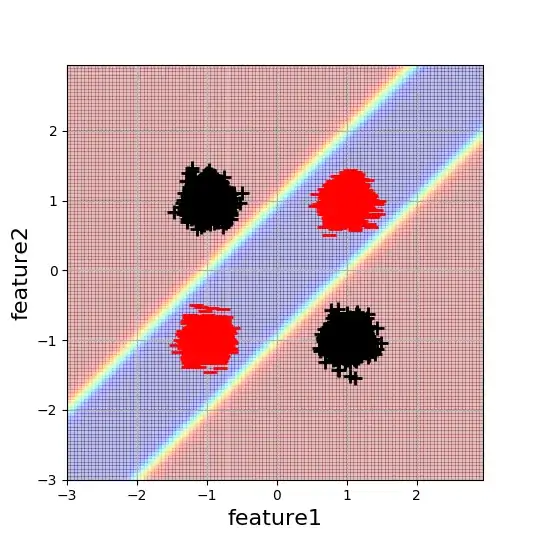
Each blob consists of 5000 data points. The minimal complexity neural network to solve this problem is a one-hidden layer network with 2 hidden neurons. Since this architecture has the minimum number of parameters possible to solve this problem (with a NN) I would naively expect that this is also the easiest to optimise. However, this is not the case.
I found that with random initialization this architecture converges around half of the time, where convergence depends on the signs of the weights. Specifically, I observed the following behaviour:
w1 = [[1,-1],[-1,1]], w2 = [1,1] --> converges
w1 = [[1,1],[1,1]], w2 = [1,-1] --> converges
w1 = [[1,1],[1,1]], w2 = [1,1] --> finds only linear separation
w1 = [[1,-1],[-1,1]], w2 = [1,-1] --> finds only linear separation
This makes sense to me. In the latter two cases the optimisation gets stuck in suboptimal local minima. However, when increasing the number of hidden neurons to values greater than 2, the network develops a robustness to initialisation and starts to reliably converge for random values of w1 and w2. You can still find pathological examples, but with 4 hidden neurons the chance that one "path way" through the network will have non-pathological weights is larger. But happens to the rest of the network, is it just not used then?
Does anybody understand better where this robustness comes from or perhaps can offer some literature discussing this issue?
Some more information: this occurs in all training settings/architecture configurations I have investigated. For instance, activations=Relu, final_activation=sigmoid, Optimizer=Adam, learning_rate=0.1, cost_function=cross_entropy, biases were used in both layers.