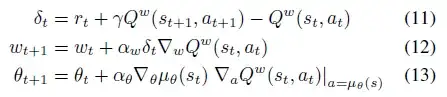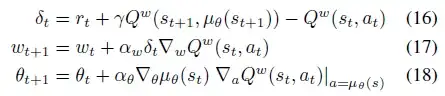In the paper Deterministic Policy Gradient Algorithms, I am really confused about chapter 4.1 and 4.2 which is "On and off-policy Deterministic Actor-Critic".
I don't know what's the difference between two algorithms.
I only noticed that the equation 11 and 16 are different, and the difference is the action part of Q function where is $a_{t+1}$ in equation 11 and $\mu(s_{t+1})$ in equation 16. If that's what really matters, how can I calculate $a_{t+1}$ in equation 11?
The twist here is that the $a_{t+1}$ in (11) and the $\mu(s_{t+1})$ in (16) are the same and actually the $a_t$ in the on-policy case and the $a_t$ in the off-policy case are different.
The key to the understanding is that in on-policy algorithms you have to use actions (and generally speaking trajectories) generated by the policy in the updating steps (to improve the policy itself). This means that in the on-policy case $a_i = \mu(s_{i})$ (in equations 11-13).
Whereas in the off-policy case you can use any trajectory to improve your value/action-value functions, which means that the actions $a_t$ can be generated by any distribution $a_t~\pi(s_t,a_t)$. In (16) the algorithm explicitly states however that the action-value function ($Q^w$) has to be evaluated at $\mu_{s_{t+1}}$ (just like in the on-policy case) and not at $a_t$ which was the actual action in the trajectory generated by policy $\pi$.
The main difference between on-policy and off-policy is how to get samples and what policy we optimize.
In off-policy deterministic actor-critic, the trajectories are samples from beta distribution (also called behavior policy), not the policy we are optimized (that is $\mu_{\theta}$). However, in the on-policy actor-critic, the action $a_{t+1}$ is sampled from target policy $\mu_{\theta}$ and the policy we optimized is also the $\mu_{\theta}$.
