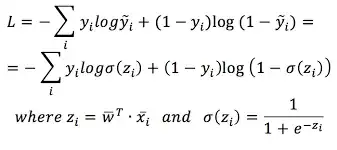Cross entropy loss is given by:
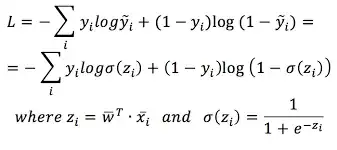
Now as we know sigmoid function outputs values between 0-1, but what you have missed is it cannot output values exactly 0 or exactly 1 as for that to happen sigmoid(z) will have to be + or -infinity.
Although your compiler gives a divide by 0 error, as very small floating point numbers are rounded off to 0, it is practically of no importance as it can happen in 2 cases only:
sigmoid(z) = 0,in which case even though the compiler cannot calculate log(0) (the first term in the equation) it is ultimately getting multiplied by y_i which will be 0 so final answer is 0.sigmoid(z) = 1,in which case even though the compiler cannot calculate log(1-1) (the second term in the equation) it is ultimately getting multiplied by 1 - y_i which will be 0 so final answer is 0.
There are a few ways to get past this if you don't want the error at all:
- Increase the precision of your compiler to float64 or infinity if available.
- Write the program in such a way that anything multiplied by
0 is 0 without looking at the other terms.
- Write the program in a way to handle such cases in a special way.
Implementation side note: You cannot bypass divide by 0 error with your manual exception handler in most processors (AFAIK) . So you have to make sure the error does not occur at all.
NOTE: It is assumed that the random weight initialisation takes care of the fact that at the beginning of training it does not so happen that $\tilde y$ or $1-\tilde y$ is 0 while the target is exactly the opposite, it is assumed that due to good training that the output is reaching near to the target and thus the 2 cases mentioned above will hold true.
Hope this helps!