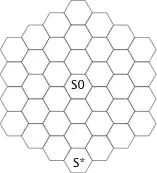
An agent aims to find a path on a hexagonal map, with an initial state $s_0$ in the center and goal state $s^*$ at the bottom as depicted below.
The map is parametrized by the distance $n \geq 1$ from $s_0$ to any of the border cells ($n = 3$ in the depicted example). The agent can move from its current cell to any of the 6 adjacent cells.
How can we find the number of node expansions performed by BFS without duplicate detection, and with duplicated detection as a function of $n$?
I know that the branching factor for the map would be 6 because the agent can move in 6 directions, and for a depth of $k$, we get $O(b^k) = 6^n$, without duplicate detection, but what is the number of node expansion with duplicate detection with BFS?