Why do we need floats for using neural networks?

Question

Is it possible to make a neural network that uses only integers by scaling input and output of each function to [-INT_MAX, INT_MAX]? Is there any drawbacks?

Answer 1

TL;DR

Not only it's possible, it even gets done and is commercially available. It's just impractical on a commodity HW which is pretty good at FP arithmetic.

Details

It is definitely possible, and you might get some speed for a lot of troubles.

The nice thing about floating point is that it works without you knowing the exact range. You can scale your inputs to the range (-1, +1) (such a scaling is pretty commonplace as it speeds up the convergence) and multiply them by 2**31, so they used the range of signed 32-bit integers. That's fine.

You can't do the same to your weights as there's no limit on them. You can assume them to lie in the interval (-128, +128) and scale them accordingly.

If your assumption was wrong, you get an overflow and a huge negative weight where a huge positive weight should be or the other way round. In any case, a disaster.

You could check for overflow, but this is too expensive. Your arithmetic gets slower than FP.

You could check for possible overflow from time to time and take a corrective action. The details may get complicated.

You could use saturation arithmetic, but it's implemented only in some specialized CPUs, not in your PC.

Now, there's a multiplication. With use of 64-bit integers, it goes well, but you need to compute a sum (with a possible overflow) and scale the output back to same sane range (another problem).

All in all, with fast FP arithmetic available, it's not worth the hassle.

It might be a good idea for a custom chip, which could do saturation integer arithmetic with much less hardware and much faster then FP.

---

Depending on what integer types you use, there may be a precision loss when compared to the floating point, which may or may not matter. Note that TPU (used in AlphaZero) has 8-bit precision only.

Answer 2

Some people might argue we can use int instead of float in NN's as float can easily be represented as anint / k where k is a multiplying factor say 10 ^ 9 e.g 0.00005 can be converted to 50000 by multiplying with 10 ^ 9..

From a purely theoretical viewpoint: This is definitely possible, but it will result in a loss of precision since int falls in the INTEGER set of number whereas floats fall in the REAL NUMBER set. Converting real numbers to int's will result in high precision loss if you are using very high precisions e.g. float64. Real numbers have an uncountable infinity, whereas integers have countable infinity and there is a well known argument called Cantor's diagonalization argument which proves this. Here is a beautiful illustration of the same. After understanding the difference you will intuitionally gain an understanding why converting int's to float is not tenable.

From a practical viewpoint: The most well known activation activation function is sigmoid activation (tanh is also very similar). The main property of these activatons are they squash numbers to between 0 and 1 or -1 and 1. If you convert floating point to a integer by multiplying with a large factor, which will result in a large number almost always, and pass it to any such function the resulting output will always almost be either of the extremities (i.e 1 or 0).

Coming to algorithms, algorithms which are similar to backpropagation with momentum cannot run on int. This is because,s since you will be scaling the int to a large number, and momentum algorithms typically use some sort of momentum_factor^n formulae, where n is the number of examples iterated already, you can imagine the result if momentum_factor = 100 and n = 10.

Only possible place where scaling might work is for relu activation. the problems with this approach will be if the data will probably not fit very good in this model, there will be relatively high errors.

Finally: All NN's do is approximate a real valued function. You can try to magnify this function by multiplying it with a factor, but whenever you are switching from, real valued function to integers you are basically representing the function as a series of steps. Something like this happens (Image only for representation purposes):

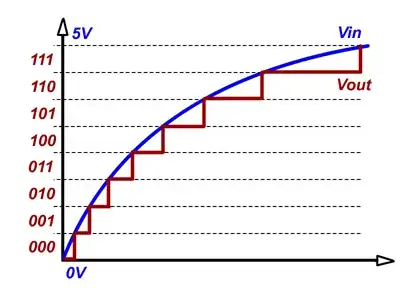
You can clearly see the problem here, each binary number represent a step, to have better accuracy you have to increase the binary steps within a given length, which in your problem will translate to having very high value of bounds [-INT_MAX, INT_MAX].

Answer 3

Floating Point Hardware

There are three common floating point formats used to approximate real numbers used in digital arithmetic circuitry. These are defined in IEEE 754, a standard that was adopted in 1985 with a revision in 2008. These mappings of bit-wise layouts real number representations are designed into CPUs, FPUs, DSPs, and GPUs either in gate level hardware, firmware, or libraries¹.

• binary 32 has a 24 bit mantissa and an 8 bit exponent
• binary 64 has a 53 bit mantissa and an 11 bit exponent
• binary 128 has a 113 bit mantissa and a 15 bit exponent²

Factors in Choosing Numerical Representations

Any of these can represent signals in signal processing, and all have been experimented with in AI for various purposes related to three things:

• Value range — not a concern in ML applications where the signal is properly normalized
• Averting saturation of the signal with rounding noise — a key issue in parameter adjustment
• Time required to execute an algorithm on a given target architecture

The balance in the best designed AI is between these last two items. In the case of back-propagation in neural nets, the gradient-based signal that approximates the desired corrective action to apply to the attenuation parameters of each layer must not become saturated with rounding noise.³

Hardware Trends Favor Floating-point

Because of the demand of certain markets and common uses, scalar, vector, or matrix operations using these standards may, in certain cases, be faster than integer arithmetic. These markets include ...

• Closed loop control (piloting, targeting, countermeasures)
• Code breaking (Fourier, finite, convergence, fractal)
• Video rendering (movie watching, animation, gaming, VR)
• Scientific computing (particle physics, astrodynamics)

First Degree Transforms to Integers

On the opposing end of numerical range, one can represent signals as integers (signed) or non-negative integers (unsigned).

In this case, the transformation between the set of real numbers, vectors, matrices, cubes, and hyper-cubes in the world of calculus⁴ and the integers that approximate them is a first degree polynomial.

The polynomial can be represented as $n = r(as + b)$, where $a \ne 0$, $n$ is the binary number approximation, $s$ is the scalar real, and $r$ is the function that rounds real numbers to the nearest integer. This defines a super-set of the concept of fixed point arithmetic because of $b$.

Integer based calculations have also been examined experimentally for many AI applications. This gives more options:

• two's complement 16 bit integer
• 16 bit non-negative integer
• two's complement 32 bit integer
• 32 bit non-negative integer
• two's complement 64 bit integer
• 64 bit non-negative integer
• two's complement 128 bit integer
• 128 bit non-negative integer

Example Case

For instance, if your theory indicates the need to represent the real numbers in the range $[-\pi, \pi]$ in some algorithm, then you might represent this range as a 64 bit non-negative integer (if that works to the advantage of speed optimization for some reason that is algorithm and possibly hardware specific).

You know that $[-\pi, \pi]$ in the closed form (algebraic relation) developed from the calculus needs to be represented in the range $[0, 2^64 - 1]$, so in $n = r(as + b)$, $a = 2^61$ and $b = 2^60$. Choosing $a = \frac {2^64} {\pi}$ would likely create the need for more lost cycles in multiplication when a simple manipulation of the base two exponent is much more efficient.

The range of values for that real number would then be [0, 1100,1001,0000,1111,1101,1010,1010,0010,0010,0001,0110,1000,1100,0010,0011,0101] and the number of bits wasted by keeping the relationship based on powers of two will be $\log_2 4 - log_2 \pi$, which is approximately 0.3485 bits. That's better than 99% conservation of information.

Back to the Question

The question is a good one, and is hardware and domain dependent.

As mentioned above hardware is continuously developing in the direction to work with IEEE floating point vector and matrix arithmetic, particularly in 32 and 64 bit floating point multiplication. For some domains and execution targets (hardware, bus architecture, firmware, and kernel), the floating point arithmetic may grossly out perform what performance gains can be obtained in 20th century CPUs by applying the above first degree polynomial transformation.

Why the Question is Relevant

In contract, if the product manufacturing price, the power consumption, and PC board size and weight must be kept low to enter certain consumer, aeronautic, and industrial markets, the low cost CPUs may be demanded. By design, these smaller CPU architectures do not have DSPs and the FPU capabilities don't usually have hardware realization of 64 bit floating point multiplication.⁵

Handling Number Ranges

Care in normalizing signals and picking the right values for a and b are essential, as mentioned, more so than with floating point, where the diminution of the exponent can eliminate many cases where saturation would be an issue with integers⁶. Augmentation of the exponent can avert overflow automatically too, up to a point, of course.

In either type of numeric representation, normalizing is part of what improves convergence rate and reliability anyway, so it should always be addressed.

The only way to deal with saturation in applications requiring small signals (such as with gradient descent in back-propagation, especially when the data set ranges are over an order of magnitude) is to carefully work out the mathematics to avoid it.

This is a science by itself, and only a few people have the scope of knowledge to handle hardware manipulation at the circuitry and assembly language level along with the linear algebra, calculus, and machine learning comprehension. The interdisciplinary skill set is rare and valuable.

---

Notes

[1] Libraries for low level hardware operations such as 128 bit multiplication are written in cross assembly language or in C with the -S option turned on so the developer can check the machine instructions.

[2] Unless you are calculating the number of atoms in the universe, the number of permutations in possible game-play for the game Go, the course to a landing pad in a crater on Mars, or the distance in meters to reach a potentially habitable planet revolving around Proxima Centauri, you will likely not need larger representations than the three common IEEE floating point representations.

[3] Rounding noise naturally arises when digital signals approach zero and the rounding of the least significant bit in the digital representation begins to produce chaotic noise of a magnitude that approaches that of the signal. When this happens, the signal is saturated in that noise and cannot be used to reliably communicate the signal.

[4] The closed forms (algebraic formulae) to be realized in software driven algorithms arise out of the solution of equations, usually involving differentials.

[5] Daughter boards with GPUs are often too pricey, power hungry, hot, heavy, and/or packaging unfriendly in non-terrestrial and consumer markets.

[6] The zeroing of feedback is skipped in this answer because it points to either one of two things: (A) Perfect convergence or (B) Poorly resolved mathematics.

Answer 4

It is possible in principle, but you will end up emulating floating point arithmetic using integers in multiple places, so it is unlikely to be efficient for general use. Training is likely to be an issue.

If the output of a layer is scaled to [-INT_MAX, INT_MAX], then you need to multiply those values by weights (which you will also need to be integers with a large enough range that learning can progress smoothly) and sum them up, and then feed them into a non-linear function.

If you are restricting yourself to integer operations only, this will involve handling multiple integers to represent high/low words in a larger int type, that you then must scale (which introduces a multi-word integer division). By the time you have done this, it is unlikely there will be much benefit to using integer arithmetic. Although perhaps it is still possible, depending on the problem, network architecture and your target CPU/GPU etc.

There are instances of working neural networks used in computer vision with only 8-bit floating point (downsampled after training). So it is definitely possible to simplify and approximate some NNs. An integer-based NN derived from a pre-trained 32-bit fp one could potentially offer good performance in certain embedded environments. I found this experiment on a PC AMD chip which showed a marginal improvement even on PC architecture. On devices without dedicated fp processing, the relative improvement should be even better.