Your probability hasn't been normalized!
In this case, you are computing the probability of being good, given that the other features have a fixed value. To obtain the correct probability, you need to normalize (divide) the value from your calculation by the probability that the features have taken on those fixed values.
You can calculate this as follows:
$$P(Fem:dv/m/s, Young, own, Ex-credpaid) = \\ \sum_{x \in \{good,bad\}} P(Fem:dv/m/s, Young, own, Ex-credpaid, x) $$
by the marginalization rule.
Then, by the chain rule, you may write:
$$\\ \sum_{x \in \{good,bad\}} P(Fem:dv/m/s, Young, own, Ex-credpaid | x) * P(x) $$
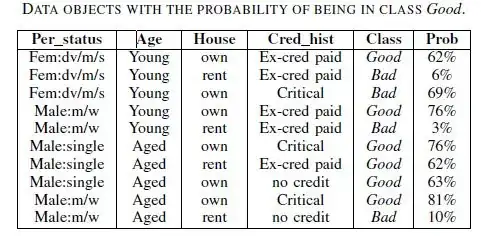
So the correct probability of 0.62 should be obtained by the equation:
$$ \frac{P(Fem:dv/m/s, Young, own, Ex-credpaid | good) * P(good)}{\sum_{x \in \{good,bad\}} P(Fem:dv/m/s, Young, own, Ex-credpaid | x) * P(x)}$$
You just need to calculate
$$P(Fem:dv/m/s, Young, own, Ex-credpaid | bad) * P(bad)$$
and it should be easy to compute the rest.