0

I'm trying to understand how the dimensions of the feature maps produced by the convolution are determined in a ConvNet.

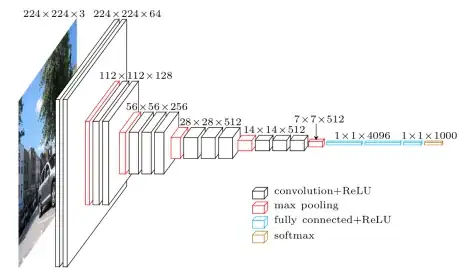
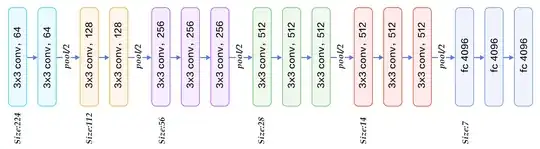
Let's take, for instance, the VGG-16 architecture. How do I get from 224x224x3 to 112x112x64? (The 112 is understandable, it's the last part I don't get)

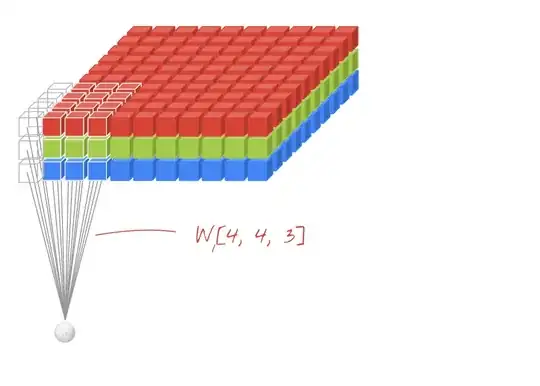
I thought the CNN was to apply filters/convolutions to layers (for instance, 10 different filters to channel red, 10 to green: are they the same filters between channels ?), but, obviously, 64 is not divisible by 3.

And then, how do we get from 64 to 128? Do we apply new filters to the outputs of the previous filters? (in this case, we only have 2 filters applied to previous outputs) Or is it something different?

vgg 16 archictecutre

nbro
  • 39,006
  • 12
  • 98
  • 176
lrosique
  • 63
  • 4

3 Answers3

1

The 64 here is the number of filters that are used. The picture is kind of misleading in that it leaves out the transition of the maxpool. enter image description here

Below is a text description of the size of the features as they go through the network with the number of filters in bold.

  1. The first 2 layers in the diagram you posted contain 64 3x3 convs resulting in a 224x224x64 matrix of features.
  2. This is then fed into a maxpool which reduces the size to a 112x112x64 matrix.
  3. This is then fed to 3 layers of 128 3x3 convs resulting in a 112x112x128 matrix.
  4. Then another maxpool giving a 56x56x128 matrix.
  5. Feeding that to 3 layers of 256 3x3 convs results in a 56x56x256 matrix.
  6. This is then fed into another maxpool giving a 28x28x256 matrix,
  7. Which is then fed into 3 layers of 512 3x3 convs resulting in a 28x28x512 matrix.
  8. Another maxpool gives a 14x14x512 matrix which is fed to 3 layers of 512 3x3 convs giving a matrix of 14x14x512 features.
  9. Another maxpool reduces this to a 7x7x512 which is then given to 3 fully connected layers of 4096 units each before being sent to a softmax.
Jaden Travnik
  • 3,767
  • 1
  • 16
  • 35
1

For learning image features with CNNs, we use 2D Convolutions. Here 2D does not refer to the input of the operation, but the output.

Consider you have an input tensor of size 224 x 224 x 3. Say for example you have 64 different convolution kernels. Theses kernels are also 3 dimensional. Each kernel will produce a 2D matrix as output. Since you have 64 different kernels/filters, you will have 64 different 2D matrices. In other words, you got a tensor with depth 64 as output.

enter image description here

I would suggest you to go through this question:

Understanding 1D, 2D and 3D convolutions

Sooryakiran Pallikulathil
  • 366
  • 2
  • 8
1

Both responses I got are correct but do not answer exactly what I was looking for.

The answer to my question is : each filter is a 2D convolution. It is applied to every channel from previous node (so we get N 2D matrices). Then all of these matrices are added up to make a final matrix (1 matrix for 1 filter). Finally, the output is all filters' matrices in parallel (like channels).

The hard part was to find the "sum up", since many websites speak of it as a 3D convolution (which is not !).

lrosique
  • 63
  • 4