From time to time I have had to do numerical work in MATLAB and the 1-based indexing always stuck out like a sore thumb, so I have a few examples I can provide where 0-based indexing is advantageous.
Modular access
This is the simplest example. If you want to "wrap around" an array, the modulus operator works like a charm. (And don't say "what if the modulus operator were defined from 1 to n instead"—that would be mathematically ludicrous.)
str = "This is the song that never ends... "
position = 300
charAtPosition = str[position % (str.length)]
Real world examples of this might include working with days of the week, generating repeating gradients, creating hash tables, or coming up with a
predicable item from a small list given a large ID number.
Distance of zero
In a lot of algorithms and applications, we need to work with distances. Distances can't be negative—but they can be zero. For example, one might want to count how many occurrences there are of each distance in a data set. Indexing from 0 allows this to be handled more naturally. (Even if distances aren't integers—see below.)
Discretisation
Let's say you want to generate a histogram of heights. The first "bucket" is 50cm-70cm. The next is 70-90cm. And so on up to 210cm.
Using zero-based indexing, the code looks like
bucket[floor((height - 50) / 20)] += 1
With 1-based indexing, it looks like
bucket[ceil((height - 50) / 20)] += 1
or
bucket[floor((height - 50) / 20) + 1] += 1
(the two have slightly different semantics). So you can either have a stray "+ 1" or use the ceil function. I believe the floor function is more "natural" than the ceil function since floor(a/b) is the quotient when you divide a by b; for this reason integer division often suffices in such calculations whereas the ceil version would be more complex. Also, if you wanted the buckets in reverse order, this is 0-based indexing:
BUCKETS = (210 - 50) / 20 - 1
#intuitive because BUCKETS - 1 is the highest index
bucket[(BUCKETS - 1) - floor((height - 50) / 20)] += 1
versus
#not intuitive... what does BUCKETS + 1 represent?
bucket[BUCKETS + 1 - ceil((height - 50) / 20)] += 1
or
#not intuitive... how come a forwards list needs "+ 1" but
#backwards list doesn't?
bucket[BUCKETS - floor((height - 50) / 20)] += 1
Change of Coordinate Systems
This is related to the above "direction flip". Although I will use a 1 dimensional example, this also applies to 2D and higher dimensional translations, rotations, and scaling.
Let's suppose, for each slot in the top row you want to find find the best fitting slot in the bottom row. (This often occurs when you want to efficiently reduce the quality of some data; image resizing is a 2D version of this).
With 0-based indexing:
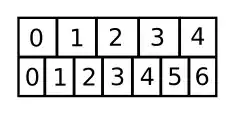
#intuitive because the centre of slot[0] is actually at x co-ordinate 0.5
nearest = floor((original + 0.5) / 5 * 7);
With 1-based indexing:
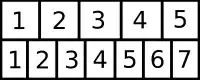
#Why -0.5? Can you explain? And then we need to "fix" it with a +1
nearest = floor((original - 0.5) / 5 * 7) + 1;
Nice Invariants
In order to prove that programs work correctly, computer scientists use the concept of an "invariant"—a property that is guaranteed to be true at a certain place in the code, no matter the program flow up to that point.
This is not just a theoretical concept. Even if invariants are not explicitly provided, code that has nice invariants tends to be easier to think about and explain to others.
Now, when writing 0-based loops, they often have an invariant that relates a variable to how many items have been processed. E.g.
i = 0
#invariant: i contains the number of characters collected
while not endOfInput() and i < 10:
# invariant: i contains the number of characters collected
input[i] = getChar()
# (invariant temporarily broken)
i += 1
#invariant: i contains the number of characters collected
#invariant: i contains the number of characters collected
There are two basic ways to write the same loop with 1-based indexing:
i = 1
while not endOfInput() and i <= 10:
input[i] = getChar()
i += 1
In this case i does not represent the number of characters collected, so the invariant is a bit messier. (You would have to remember to subtract one later on if you wanted the count.) Here is the other way:
i = 0
while not endOfInput() and i < 10:
i += 1
input[i] = getChar()
Now the invariant holds again so this approach seems preferable, but it seems odd that the initial value of i can't be used as an array index—that we are not "ready to go" straight away and have to fix up i first. I suppose it's initially odd for learners of zero-based languages that, after the loop terminates, the variable is one more than the highest index used, but it all follows from the basic rule of "a list of size i can be indexed from 0 to i-1".
I admit that these arguments may not be very strong. That said, off-by-1 errors are one of the most common types of bug and at least in my experience, starting arrays from 1 needs a whole lot more adding and subtracting 1 than 0-based arrays.