Complex Analysis/Curves

Introduction

In the Mathematics a curve (of lat. curvus for "bent", "curved") is a one dimensionals object in a two-dimensional plane (i.e. a curve in the plane) or in a higher-dimensional space.

Parameter representations

• Multidimensional analysis: A continuous mapping ${\textstyle f:[a,b]\to \mathbb {R} ^{n}}$ is a curve in the ${\textstyle \mathbb {R} ^{n}}$.
• Complex Analysis: Continuous mapping ${\textstyle f:[a,b]\to \mathbb {C} }$ is a path in ${\textstyle \mathbb {C} }$ (see also path for integration).

Explanatory notes

A curve/a way is a mapping. It is necessary to distinguish the track of the path or the image of a path from the mapping graph. A path is a steady mapping of a interval in the space considered (e.g. ${\textstyle \mathbb {R} ^{n}}$ or ${\textstyle \mathbb {C} }$).

Curve as Image of Path

Let ${\textstyle \gamma$ :[a,b]\to \mathbb {C} } or ${\textstyle \gamma$ :[a,b]\to \mathbb {R} ^{n}} be a path. is the image of a path

${\textstyle Trace(\gamma ):=\left\{\gamma (t)\ |\ a\leq t\leq b\right\}}$.

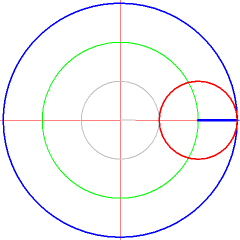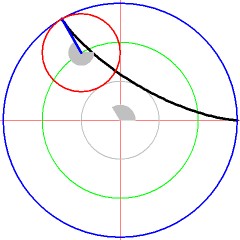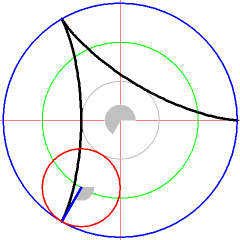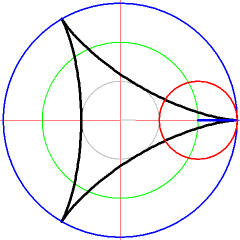
Curves in Geogebra

First create a slider for the variable ${\textstyle t\in [0,2\pi ]}$ and two points ${\textstyle K_{1}=(2\cos(t),2\sin(t))\in \mathbb {R} ^{2}}$ or ${\textstyle K_{2}=(\cos(3t),\sin(3t))\in \mathbb {R} ^{2}}$ and generate with ${\textstyle K:=K_{1}+K_{2}}$ the sum of both location vectors of ${\textstyle K_{1}}$ and ${\textstyle K_{2}}$. Analyze the parameterization of the curves.

  K_1:(2*cos(t),2 * sin(t)) 
  K_2:(cos(3*t),sin(3*t))
  K: K_1+K_2 

Representations of Image Sets by Equations

A curve can also be described by one or more equations in the coordinates. The solution of the equations represents the curve:

• The equation ${\textstyle x^{2}+y^{2}=1}$ describes the unit circle in the plane.
• The equation ${\textstyle y^{2}=x^{2}(x+1)}$ describes the curve indicated above in parameter representation with double point.

If the equation is given by a Polynomial, the curve is called algebraic.

Graph of a function

Functiongraphs are a special case of the two forms indicated above: The graph of a function

${\textstyle f\colon D\to \mathbb {R} ,\quad x\mapsto f(x)}$

can be either as a parameter representation ${\textstyle \gamma \colon D\to \mathbb {R} ^{2},\quad t\mapsto (t,f(t))\}}$ or as equation ${\textstyle y=f(x)}$, wherein the solution quantity of the equation represents the curve by ${\textstyle \{(x,y)\in \mathbb {R} ^{2}\mid y=f(x)\}}$. If theMathematics education of Curve sketching is spoken, this special case is usually only said.

Closed curves

Closed curves ${\textstyle \gamma \colon [a,b]\to \mathbb {C} }$ are continuous mappings with ${\textstyle \gamma (a)=\gamma (b)}$. In the function theory, we need curves ${\textstyle \gamma \colon [a,b]\to \mathbb {C} }$ in ${\textstyle \mathbb {C} }$, which can be continuously differentiated. These are called integration paths.

Curves as Independent Objects

Curves without an ambient space are relatively uninteresting in w:en:Differential Geometry because every one-dimensional manifold is diffeomorphic to the real line ${\displaystyle \mathbb {R} }$ or to the unit circle ${\displaystyle S^{1}}$. Also, properties like the curvature of a curve are intrinsically undetectable.

In algebraic geometry and, correspondingly, in complex analysis, "curves" typically refer to one-dimensional complex manifolds, often also called Riemann surfaces. These curves are independent objects of study, with the most prominent example being elliptic curves. See curve (algebraic geometry)

Historical

The first book of Elements by Euclid began with the definition:

"A point is that which has no parts. A curve is a length without breadth."

This definition can no longer be upheld today because, for example, there are Peano curves, i.e., continuous surjective mappings ${\displaystyle f\colon \mathbb {R} \to \mathbb {R} ^{2}}$ that fill the entire plane ${\displaystyle \mathbb {R} ^{2}}$. On the other hand, the Sard's Lemma implies that every differentiable curve has zero area, i.e., as Euclid demanded, it truly has no breadth.

Interactive Representations of Curves in GeoGebra

• Tangent vector of a curve in ${\displaystyle \mathbb {R} ^{2}}$ for a curve ${\displaystyle \gamma$ :[a,b]\to \mathbb {R} ^{2}} with tangent vector ${\displaystyle \gamma ':[a,b]\to \mathbb {R} ^{2}}$

• Rolling curves Bicycle reflectors as an example of curves - Cycloid

• Rolling curve for Example 2

See also

• Space curves in ${\displaystyle \mathbb {R} ^{3}}$

• Curves in geometry

• Differentiable curves, curvature

• Cycloid

Literature

• Ethan D. Bloch: A First Course in Geometric Topology and Differential Geometry. Birkhäuser, Boston 1997.

• Wilhelm Klingenberg: A Course in Differential Geometry. Springer, New York 1978.

References

1. ↑ H. Neunzert, W.G. Eschmann, A. Blickensdörfer-Ehlers, K. Schelkes: Analysis 2: Mit einer Einführung in die Vektor- und Matrizenrechnung. Ein Lehr- und Arbeitsbuch. 2. Auflage. Springer, 2013, lSBN 978-3-642-97840-1, 23.5
2. ↑ H. Wörle, H.-J. Rumpf, J. Erven: Taschenbuch der Mathematics. 12. Auflage. Walter de Gruyter, 1994, lSBN 978-3-486-78544-9

External Links

Wikimedia Commons has media related to Kurven.

Look up Kurve in Wiktionary, the free dictionary.

Page Information

You can display this page as Wiki2Reveal slides