Complex Numbers/From real to complex numbers

Introduction

This page about Complex Numbers/From real to complex numbers can be displayed as Wiki2Reveal slides. Single sections are regarded as slides and modifications on the slides will immediately affect the content of the slides. The following aspects of Complex Numbers/From real to complex numbers are considered in detail:

(1) Real numbers embedded in plane of complex numbers
(2) geometric aspects of algebraic operations in $\mathbb {C}$

Extension of the number range

The complex numbers ${\textstyle \mathbb {C} }$ extend the number range of the real numbers in such a way that the equation ${\textstyle x^{2}=-1}$ can be solved. The equation ${\textstyle x^{2}=-1}$ has no solution in $\mathbb {R}$ . The solubility is accomplished by introducing a new imaginary number ${\textstyle \mathrm {i} }$ with the property ${\textstyle \mathrm {i} ^{2}=-1}$ . This number ${\textstyle \mathrm {i} }$ is referred to as imaginary unit.

Algebraic expression for complex numbers

Complex numbers can be defined in the form ${\textstyle z=x+y\cdot \mathrm {i} }$ , where ${\textstyle x,y\in \mathbb {R} }$ are respectively real numbers and ${\textstyle \mathrm {i} }$ is the imaginary unit. The identification with a vector ${\textstyle (x,y)\in \mathbb {R} ^{2}}$ can be used to represent complex numbers in a coordinate system (Gaußian number level).

Real part and imaginary part

The real-valued coefficients ${\textstyle x,y}$ are referred to as real part or imaginary part of a complex number ${\textstyle z=x+y\,\mathrm {i} }$ .

${\textstyle x=\operatorname {Re} (z)=\operatorname {Re} (x+y\,\mathrm {i} )}$ and
${\textstyle y=\operatorname {Im} (z)=\operatorname {Im} (x+y\,\mathrm {i} )}$

Gaussian Plane

With the identification of $x+iy\in \mathbb {C}$ with $(x,y)\in \mathbb {R} ^{2}$ we can draw a complex number in plane.

Gaussian coordinatesystem

Polar coordinates

The following equations show the link between exponential functions and trigonometric functions:

z=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }=r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )

which results from ${\textstyle a=r\cdot \cos \varphi }$ and ${\textstyle b=r\cdot \sin \varphi }$ .

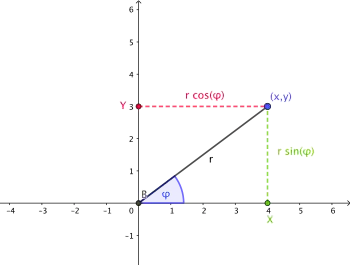
Polar coordinates

Polarcoordinates and Cartesian coordinate system

Exponential function and trigonometry

The representation with the aid of the complex e-function ${\textstyle r\cdot \mathrm {e} ^{\mathrm {i} \varphi }}$ also means exponential representation (the polar form), the representation by means of the expression ${\textstyle r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )}$ geometric representation (the polar form).

Characteristics

The set of the complex numbers forms a extension of the field of the real numbers. The set of complex numbers is a field with $\mathbb {R} \subset \mathbb {C}$ and has geometric and some algebraic properties that are not valid in field of real values ${\textstyle \mathbb {R} }$

Fundamental theorem of algebra

The complex numbers are algebraically completed^[1]^[2]. This theorem states that every non-constant single-variable polynomial with complex coefficients has at least one complex root.

Remark - Polynomials with real-valued coefficients

The theorem is also applicable for polynomials with real-valued coefficients, since every real number is a complex number with its imaginary part equal to zero.

Example

In ${\textstyle \mathbb {C} }$ the following algebraic equations with a polynomial with real-valued coefficient has no solution in ${\textstyle \mathbb {R} }$ but two solutions in the complex numbers.

{\textstyle x^{2}+4=0}

(see [[w:en:Fundamental theorem of algebra).

Trigonometry and exponential function

In ${\textstyle \mathbb {C} }$ the relationship between trigonometric functions and Exponential function is defined with following equation:

\mathrm {e} ^{\mathrm {i} t}=\cos(t)+\mathrm {i} \cdot \sin(t)

see Euler's formula.

Difference: complex and real differentiation

On an open set all complex differentiable functions can also be differentiated in the real number. In calculus on the real numbers the following function

{\textstyle f(x)=x^{2}\cdot |x|}

can be differentiated 2x and the thrid derivation does not exist. If we consider ${\textstyle f:\mathbb {C} \to \mathbb {C} }$ then $f$ is just a continuous function on $\mathbb {C}$ but in none of the points $z\in \mathbb {C}$ complex differentiable.

Partial relationship between real and complex numbers

The real numbers can be considered as a subset of the complex numbers in the sense of a subset of complex numbers. In this context a real number ${\textstyle x\in \mathbb {R} }$ is identified with the complex number ${\textstyle x+0\mathrm {i} \in \mathbb {C} }$ . In the Gaussian plane, the real numbers corresponded to the points on the ${\textstyle x}$ axis.

Complex conjugation

Changing the sign of the imaginary part ${\textstyle y}$ of a complex number ${\textstyle z=x+y\,\mathrm {i} ,}$ leads to the complex conjugation ${\overline {z}}$ of a complex number $z$ . ${\overline {z}}$ can be created by reflection of $z$ at the x axis of the plane.

Computing the Conjugation

The conjugation ${\textstyle \mathbb {C} \to \mathbb {C} ,\,z\mapsto {\bar {z}}}$ is a [[w:en:Involution (Mathematics)|(involutoric)] body automorphism, since it is compatible with addition and multiplication, i.e., for all $y,z\in \mathbb {C}$

{\textstyle {\overline {y+z}}={\bar {y}}+{\bar {z}},\quad {\overline {y\cdot z}}={\bar {y}}\cdot {\bar {z}}.}

Geometric representation of conjugation

In the polar representation, the conjugated complex number ${\textstyle {\bar {z}}}$ has an unchanged distance to the coordinate origin (i.e. ${\textstyle |{\bar {z}}|=|z|}$ ) and has the negative angle of ${\textstyle z}$ . The conjugation in the complex numerical plane can therefore be interpreted as the 'mirror at the real axis'. In particular, under conjugation exactly the real numbers are mapped onto themselves.

Geometric representation of conjugation

A complex number ${\textstyle z=x+\mathrm {i} \cdot y}$ and the complex number conjugated to it ${\textstyle {\bar {z}}=x-\mathrm {i} \cdot y}$

Conjugation in Gaussian Plane

Absolute Value

The Absolute Value ${\textstyle |z|}$ of a complex number ${\textstyle z}$ is the length of its vector in the Gaussian plane or complex plane. The

|z|={\sqrt {x^{2}+y^{2}}}

calculate from their real part ${\textstyle \operatorname {Re} (z)=a}$ and imaginary part ${\textstyle \operatorname {Im} (z)=b}$ . As a length, the amount is real and not negative.

Example - Absolute Value of a complex number

{\textstyle |239+\mathrm {i} |={\sqrt {239^{2}+1^{2}}}={\sqrt {57121+1}}={\sqrt {57122}}=169\cdot {\sqrt {2}}}

Pythagorean theorem

The real part ${\textstyle x\in \mathbb {R} }$ and the imaginary part ${\textstyle y\in \mathbb {R} }$ of a complex number can be interpreted as the the catheti of right triangle where the length of hypotenuse is geometrically the absolute value of the complex number.

|z|={\sqrt {x^{2}+y^{2}}}

Characteristics

In ${\textstyle (\mathbb {C} ,+,\cdot )}$ the following properties apply:

(AG/KG) The Assoziative Law and Commutative Law apply to the addition and multiplication of complex numbers.
(DG) The Distributive Law applies.
'(NE) O and 1 are the neutral elements of the addition resp. of the multiplication.
(IE ${\textstyle +}$ ) For every complex number $z$ there is a complex number ${\textstyle (-z)}$ with $z+(-z)=-z+z=0$ .
(IE ${\textstyle \cdot }$ ) For each complex number different from zero ${\textstyle z}$ exists a complex number ${\textstyle z^{-1}}$ with ${\textstyle z\cdot z^{-1}=z\cdot z=1}$

Calculation - algebraic form

The algebraic properties result directly from the definition of the two links.

Addition

For the addition of two complex numbers ${\textstyle z_{1}=a_{1}+b_{1}\,\mathrm {i} }$ with ${\textstyle a,b\in \mathbb {R} }$ and ${\textstyle z_{2}=a_{2}+b_{2}\,\mathrm {i} }$

z_{1}+z_{2}=(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathrm {i} .

Vector Space - Visualization Addition

The addition of two complex numbers in the complex plane

Subtraction

For the subtraction of two complex numbers ${\textstyle z_{1}}$ and ${\textstyle z_{2}}$ (see addition) applies

z_{1}-z_{2}=(a_{1}-a_{2})+(b_{1}-b_{2})\,\mathrm {i} .

Multiplication

For the multiplication of two complex numbers ${\textstyle z_{1}}$ and ${\textstyle z_{2}}$ (see addition) applies

{\begin{array}{rcl}z_{1}\cdot z_{2}&=&(a_{1}a_{2}+b_{1}b_{2}\,\mathrm {i} ^{2})+(a_{1}b_{2}+a_{2}b_{1})\,\mathrm {i} \\&=&(a_{1}a_{2}-b_{1}b_{2})+(a_{1}b_{2}+a_{2}b_{1})\,\mathrm {i} \\\end{array}}

Division

For the division of the complex number ${\textstyle z_{1}}$ by the complex number ${\textstyle z_{2}}$ with ${\textstyle z_{2}\neq 0}$ the multiplication with the complex conjugate denominator for the numerator and denominator of the fraction. This results in a real valued denominator as the square of the absolute value of ${\textstyle z_{2}=a_{2}+b_{2}\,\mathrm {i} }$ ):

{\textstyle {\frac {z_{1}}{z_{2}}}={\frac {(a_{1}+b_{2}\,\mathrm {i} )(a_{2}-b_{2}\,\mathrm {i} )}{(a_{2}+b_{2}\,\mathrm {i} )(a_{2}-b_{2}\,\mathrm {i} )}}=={\frac {a_{1}a_{2}+b_{1}b_{2}}{a_{2}^{2}+b_{2}^{2}}}+{\frac {b_{1}a_{1}-a_{1}b_{2}}{a_{2}^{2}+b_{2}^{2}}}\mathrm {i} .}

Computation Example Addition:

{\textstyle (3+2\mathrm {i} )+(5+5\mathrm {i} )=(3+5)+(2+5)\mathrm {i} =8+7\mathrm {i} }

Subtraction example:

{\textstyle (5+5\mathrm {i} )-(3+2\mathrm {i} )=(5-3)+(5-2)\mathrm {i} =2+3\mathrm {i} }

Multiplication calculation example:

{\textstyle (3+5\mathrm {i} )\cdot (4+11\mathrm {i} )=(3\cdot 4-5\cdot 11)+(3\cdot 11+5\cdot 4)\mathrm {i} =-43+53\mathrm {i} }

Computational Example Division:

{\textstyle {{\frac {(2+5\mathrm {i} )}{(3+7\mathrm {i} )}}={\frac {(2+5\mathrm {i} )}{(3+7\mathrm {i} )}}\cdot {\frac {(3-7\mathrm {i} )}{(3-7\mathrm {i} )}}}=}

{\textstyle ={{\frac {(6+35)+(15\mathrm {i} -14\mathrm {i} )}{(9+49)+(21\mathrm {i} -21\mathrm {i} )}}={\frac {41+\mathrm {i} }{58}}={\frac {41}{58}}+{\frac {1}{58}}\cdot \mathrm {i} }}

Learning Activity

Be given ${\textstyle z=z_{1}+\mathrm {i} z_{2}\in \mathbb {C} \setminus \{0\}}$ . Solve the equation:

{\textstyle z\cdot x=1=1+0\mathrm {i} }

with

{\textstyle x=x_{1}+ix_{2}\in \mathbb {C} }

and

{\textstyle x_{1},x_{2}\in \mathbb {R} }

Two complex numbers are the same when they match the real part and imaginary part. This creates a equation system with two equations and the two unknowns ${\textstyle x_{1},x_{2}\in \mathbb {R} }$

Complex numbers as a real vector space

The body ${\textstyle \mathbb {C} }$ of the complex numbers is on the one hand an upper body of ${\textstyle \mathbb {R} }$ , on the other hand a two-dimensional ${\textstyle \mathbb {R} }$ ve:en:vector space Isomorphism ${\textstyle \mathbb {C} \cong \mathbb {R} ^{2}}$ is also referred to as natural identification.

Base of vector space

As ${\textstyle \mathbb {R} }$ -vector space owns ${\textstyle \mathbb {C} }$ the base ${\textstyle \{1,\mathrm {i} \}}$ . In addition, ${\textstyle \mathbb {C} }$ is like each body also a vector space over itself, i.e. a one-dimensional ${\textstyle \mathbb {C} }$ -vector space with base ${\textstyle \{1\}}$ .

Order - complex numbers

${\textstyle \mathbb {C} }$ does not have (in contrast to ${\textstyle \mathbb {R} }$ ) no order, i.e., there is complete order relation to two complex numbers.

Links between Representations of Complex Numbers

Gaussian plane with a complex number in Cartesian coordinates (a,b) and in polar coordinates (r,φ)

Algebraic Structure - Polar coordinates

While the set ${\textstyle \mathbb {R} }$ of the real numbers can be illustrated by points on a number line, the set ${\textstyle \mathbb {C} }$ corresponds to as a two-dimensional real vector space ${\textstyle \mathbb {C} }$ .

Polar coordinates

Points - Vectors

According to the definition, the addition of complex numbers corresponds to the vector addition, the points in the number plane being identified with their [[w:en:location vector]en. The multiplication is a w:en:rotational stretching in the outer plane, which will become clearer after the introduction of the polar form (see Geogebra example).

Conversion formulae: algebraic shape into the polar shape

For ${\textstyle z=a+b\,\mathrm {i} }$ is in algebraic form

r=|z|={\sqrt {a^{2}+b^{2}}}={\sqrt {z\cdot {\overline {z}}}}.

For ${\textstyle z=0}$ the argument can be defined with 0, but usually remains undefined. For ${\textstyle z\neq 0}$ , the argument ${\textstyle \varphi }$ in the interval ${\textstyle (-\pi$ can be used with the aid of a triArgonometric reversal function, e.

\varphi =\arg(z)={\begin{cases}\arccos {\frac {a}{r}}&\mathrm {f{\ddot {u}}r} \ b\geq 0\\-\arccos {\frac {a}{r}}&{\text{sonst}}\end{cases}}

to be determined.

Conversion formulae: Polar form into algebraic form

{\textstyle a={\mathfrak {Re}}(z)=r\cdot \cos \varphi }

{\textstyle b={\mathfrak {Im}}(z)=r\cdot \sin \varphi }

As above, ${\textstyle a\in \mathbb {R} }$ represents the real part and ${\textstyle b\in \mathbb {R} }$ the imaginary part of the complex number ${\textstyle z=a+ib\in \mathbb {C} }$ .

Arithmetic operations in the polar form

By arithmetic operations, the following operands are to be linked to one another:

z_{1}=r\cdot (\cos \varphi +\mathrm {i} \cdot \sin \varphi )=r\cdot \mathrm {e} ^{\mathrm {i} \varphi }

z_{2}=s\cdot (\cos \psi +\mathrm {i} \cdot \sin \psi )=s\cdot \mathrm {e} ^{\mathrm {i} \psi }

In the case of multiplication, the absolute values ${\textstyle r}$ and ${\textstyle s}$ are multiplied for the product and the angles ${\textstyle \varphi }$ and ${\textstyle \psi }$ are added. For the division/fraction, the absolute values are divided ${\frac {r}{s}}$ and the angles are substracted.

{\frac {z_{1}}{z_{2}}}={\frac {r}{s}}\cdot e^{\mathrm {i} \cdot (\varphi -\psi )}

Trigonometric Form - Multiplication

{\textstyle {z_{1}\cdot z_{2}=r\cdot s\cdot \left(\cos(\varphi +\psi )+\mathrm {i} \cdot \sin(\varphi +\psi )\right)}}

Trigonometric form - Division

{\textstyle {\frac {z_{1}}{z_{2}}}={\frac {r}{s}}\cdot \left(\cos(\varphi -\psi )+\mathrm {i} \cdot \sin(\varphi -\psi )\right)}

Exponential Expression

${\textstyle z_{1}\cdot z_{2}=r\cdot s\cdot \mathrm {e} ^{\mathrm {i} (\varphi +\psi )}}$
${\textstyle {\frac {z_{1}}{z_{2}}}={\frac {r}{s}}\cdot \mathrm {e} ^{\mathrm {i} (\varphi -\psi )}}$

Real part and imaginary part function

Be ${\textstyle f:V\to \mathbb {C} }$ This defines the real part function and imaginary part function as a relative image as follows.

${\textstyle g:V\to \mathbb {R} }$ with ${\textstyle g(z):={\mathfrak {Re}}(f(z))}$ and ${\textstyle h:V\to \mathbb {R} }$
${\textstyle f(z)=g(z)+i\cdot h(z)}$ for all ${\textstyle z\in V}$

Literature

Paul Nahin: An imaginary tale. The story of ${\textstyle {\sqrt {-1}}}$ . Princeton University Press, 1998.
Reinhold Remmert: complex numbers. In D. Ebbinghaus et al. (Eds.): Numbers. Springer, 1983.

Sources of literature

↑ Dunham, William (September 1991), "Euler and the fundamental theorem of algebra" (PDF), The College Journal of Mathematics, 22 (4): 282–293, JSTOR 2686228
↑ Campesato, Jean-Baptiste (November 4, 2020), "14 - Zeroes of analytic functions" (PDF), MAT334H1-F – LEC0101, Complex Variables, University of Toronto, retrieved 2024-09-05

Page Information

You can display this page as Wiki2Reveal slides

Wiki2Reveal

The Wiki2Reveal slides were created for the Complex Numbers' and the Link for the Wiki2Reveal Slides was created with the link generator.

This page is designed as a PanDocElectron-SLIDE document type.
Source: Wikiversity https://en.wikiversity.org/wiki/Complex%20Numbers/From%20real%20to%20complex%20numbers
see Wiki2Reveal for the functionality of Wiki2Reveal.

Translation and Version Control

This page was translated based on the following Wikiversity source page and uses the concept of Translation and Version Control for a transparent language fork in a Wikiversity:

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Dunham, William (September 1991), "Euler and the fundamental theorem of algebra" (PDF), The College Journal of Mathematics, 22 (4): 282–293, JSTOR 2686228

[2] Campesato, Jean-Baptiste (November 4, 2020), "14 - Zeroes of analytic functions" (PDF), MAT334H1-F – LEC0101, Complex Variables, University of Toronto, retrieved 2024-09-05

[1]

[2]

Complex Numbers/From real to complex numbers

Introduction

Extension of the number range

Algebraic expression for complex numbers

Real part and imaginary part

Gaussian Plane

Polar coordinates

Polar coordinates

Exponential function and trigonometry

Characteristics

Fundamental theorem of algebra

Remark - Polynomials with real-valued coefficients

Example

Trigonometry and exponential function

Difference: complex and real differentiation

Partial relationship between real and complex numbers

Complex conjugation

Computing the Conjugation

Geometric representation of conjugation

Geometric representation of conjugation

Absolute Value

Example - Absolute Value of a complex number

Pythagorean theorem

Characteristics

Calculation - algebraic form

Addition

Vector Space - Visualization Addition

Subtraction

Multiplication

Division

Computation Example Addition:

Subtraction example:

Multiplication calculation example:

Computational Example Division:

Learning Activity

Complex numbers as a real vector space

Base of vector space

Order - complex numbers

Links between Representations of Complex Numbers

Algebraic Structure - Polar coordinates

Points - Vectors

Conversion formulae: algebraic shape into the polar shape

Conversion formulae: Polar form into algebraic form

Arithmetic operations in the polar form

Trigonometric Form - Multiplication

Trigonometric form - Division

Exponential Expression

Real part and imaginary part function

Literature

See also

Sources of literature

Page Information

Wiki2Reveal

Translation and Version Control