Cube root

Introduction

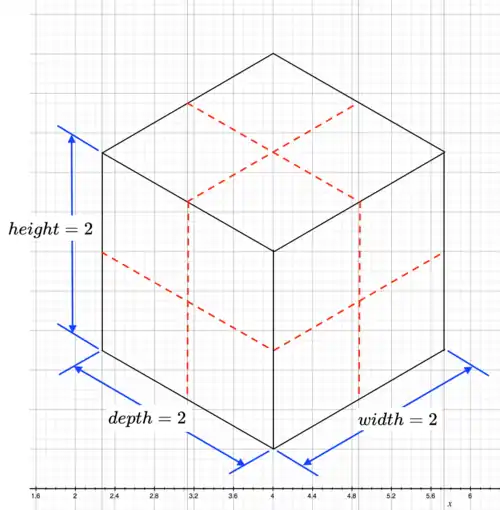
Diagram of cube (in solid black lines.)
The diagram shows the relationship of width, depth or height to surface area and volume.

A cube is a regular solid in three dimensions with depth, width and height all equal.

In the diagram the figure defined by solid black lines is a cube. Width = depth = height = 2.

The length of one side is 2 units.

The surface area of one side $=\ height*depth$ or $height*width$ or $width*depth=2*2$ or $2^{2}$ square units. There are 4 square units in each side.

The volume of the cube $=\ width*depth*height\ =\ 2*2*2=2^{3}=8$ cubic units.

In this case you can see that 8 cubes of 1 unit each, when properly stacked together, form a cube with length of each side equal to 2 units and volume equal to 8 cubic units.

In mathematical terms $V=s^{3}=2^{3}=8.$

We can say that $V=s$ raised to the power of 3. Usually we say that $V=s$ cubed.

The calculation of cube root is the process reversed. Given $V$ or volume, what is the length of each side?

$s=V^{\frac {1}{3}}$ read as $s=V$ raised to the power ${\frac {1}{3}}.$ Usually we say that $s={\sqrt[{3}]{V}}$ or $s=$ cube root of $V.$

In this case $s={\sqrt[{3}]{8}}=2.$

When $s={\sqrt[{3}]{V}}$ then $s^{3}=({\sqrt[{3}]{V}})^{3}=(V^{1/3})^{3}=V^{\frac {3}{3}}=V^{1}=V.$

If $s$ is negative, then $(-s)^{3}=(-s)*(-s)*(-s)=-(s*s*s)=-V$ and ${\sqrt[{3}]{-V}}=-s.$

In theoretical math the cube root of any real number has 3 values, 1 real and 2 complex.

On this page, we'll refer to the one real value noting that the cube root of a negative real number is also a negative real number.

Calculation

Preparation

It is desired to calculate the cube root of real number $N.$

To simplify the process, and to make the implementation of the process predictable, reformat $N:$

$N=n(10^{3p})$ where:

$1\leq n<1000$

$p$ is integer.

Then: ${\sqrt[{3}]{N}}={\sqrt[{3}]{n(10^{3p})}}={\sqrt[{3}]{n}}(10^{p}).$

To simplify the process further, we calculate cube root of abs(n) and restore negative sign to result, if necessary.

# python code.

import decimal
dD = decimal.Decimal
dgt = decimal.getcontext()
desired_precision = 100     # Adjust as necessary.
Precision = dgt.prec = desired_precision + 3

NormalizeNumberDebug = 0

def NormalizeNumber (number, flag = 0) :
    '''
sign, newNumber, exponent = NormalizeNumber (number [, flag])
sign & exponent are both ints.
newNumber is Decimal object.
1000 > newNumber >= 1 and
exponent % 3 = 0.
This prepares number for cube root of number.
eg, 1234.56e-2 becomes 123456e-4, 12345600e-6, 12.345600e0, 12.3456e0
    123.456e7 becomes 123456e4, 1234560e3, 1.234560e9, 1.23456e9
'''
    thisName = 'NormalizeNumber () :'
    
    if NormalizeNumberDebug : flag_ = NormalizeNumberDebug
    else : flag_ = flag
    print_ = flag_ & 1 ; print_all = flag_ & 2 ; check = flag_ & 4
    if print_all : print_ = 1
    if print_ : check = 4

    number = dD(str(number))
    if print_ :
        print()
        print(thisName)
        print('  Input number =',number)
    if print_all :
        print('  flag_ =', bin(flag_))

    if number == 0 : return (0, dD(0), 0)

    sign, digits, exponent = tuple(number.as_tuple())

    if print_all :
        print (' ', digits)
        print ('  exponent =', exponent)
    digits = list(digits)

    # Remove leading zeroes.
    while (digits[0] == 0) :
        digits[:1] = []
        if print_all :
            print (' ', digits)
            print ('  exponent =', exponent)

    # Remove trailing zeroes.
    while (digits[-1] == 0) :
        digits[-1:] = [] ; exponent += 1
        if print_all :
            print (' ', digits)
            print ('  exponent =', exponent)

    # Ensure that exponent is exactly divisible by 3.
    while exponent % 3 :
        digits += [0] ; exponent -= 1
        if print_all :
            print (' ', digits)
            print ('  exponent =', exponent)

    number_of_digits = len(digits)
    if number_of_digits <= 3:
        newNumber = dD ( (0,digits,0) )
    else :    
        number_of_integers = number_of_digits % 3
        if number_of_integers == 0 : number_of_integers = 3
        number_of_decimal_places = number_of_digits - number_of_integers
        digits[-number_of_decimal_places:-number_of_decimal_places] = ['.']
        exponent += number_of_decimal_places
        if print_all :
            print (' ', digits)
            print ('  exponent =', exponent)
        while (digits[-1] == 0) :
            del(digits[-1])
            if print_all :
                print (' ', digits)
                print ('  exponent =', exponent)
        newNumber = dD( ''.join([ str(v) for v in digits ]) )

    # If necessary, check.
    if check :
        str1 = str(newNumber)
        dD1 = dD( ('', '-')[sign] + str1 + 'e' + str(exponent) )
        if dD1 != number :
            # This should not happen.
            print (thisName)
            print ('  error:', dD1 , '!=', number)
            return None

    if print_ :
        print (thisName)
        print ('  Output:')
        print ('    sign =', sign)
        print ('    newNumber =', newNumber)
        print ('    exponent =', exponent)

    return sign, newNumber, exponent

Example

This example illustrates how number N is changed to conform to desired format.

# python code.

NormalizeNumber ('00123345.6789000000000000', 2)

NormalizeNumber () :
  Input number = 123345.6789000000000000
  flag_ = 0b10
  (1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)
  exponent = -16
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
  exponent = -15
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
  exponent = -14
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0, 0, 0]
  exponent = -13
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0, 0]
  exponent = -12
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0, 0]
  exponent = -11
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0, 0]
  exponent = -10
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0, 0]
  exponent = -9
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0, 0]
  exponent = -8
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0, 0]
  exponent = -7
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0]
  exponent = -6
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0]
  exponent = -5
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9]
  exponent = -4
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0]
  exponent = -5
  [1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 0, 0]
  exponent = -6
  [1, 2, 3, '.', 3, 4, 5, 6, 7, 8, 9, 0, 0]
  exponent = 3
  [1, 2, 3, '.', 3, 4, 5, 6, 7, 8, 9, 0]
  exponent = 3
  [1, 2, 3, '.', 3, 4, 5, 6, 7, 8, 9]
  exponent = 3
NormalizeNumber () :
  Output:
    sign = 0
    newNumber = 123.3456789
    exponent = 3

Implementation

$x={\sqrt[{3}]{n}}$

$x^{3}=n$

$x^{3}-n=0$

To calculate ${\sqrt[{3}]{n}}$ calculate the real root of:

$y=f(x)=x^{3}-n.$

$f(x)$ is well defined in the region $1\leq n<1000.$

If $n$ is type int and exact cube, ${\sqrt[{3}]{n}}$ is extracted from table values_of_v_and_v_cubed.

Else, Newton's method is used to derive the root starting with $x={\text{int}}({\sqrt[{3}]{n}})+1.$

# python code.

simpleCubeRootDebug = 0

def simpleCubeRoot (N, flag = 0) :
    '''
cube_root = simpleCubeRoot (N [, flag]) 

    '''
    thisName = 'simpleCubeRoot () :'

    if simpleCubeRootDebug : flag_ = simpleCubeRootDebug
    else : flag_ = flag
    print_ = flag_ & 1 ; print_all = flag_ & 2 ; check = flag_ & 4
    if print_all : print_ = 1
    if print_ : check = 4

    if print_ :
        print()
        print (thisName)
        print ('  Input N =',N)
    if print_all :
        print ('  flag_ =', bin(flag_))
    if N == 0 : return dD(0)
    if abs(N) == 1 : return dD(str(N)).normalize()

    sign1, n, exponent = NormalizeNumber (N, flag)
    if print_all :
        print (thisName)
        print ('  sign1 = {}'.format(sign1))
        print ('  n = {}'.format(n))
        print ('  exponent = {}'.format(exponent))

    if check :
        if sign1 not in (0,1) :
            print (thisName, 'Internal error 1.')
            return None
        if (1 <= n < 1000) : pass
        else :
            print (thisName, 'Internal error 2.')
            return None
        if exponent % 3 :
            print (thisName, 'Internal error 3.')
            return None
 
    # Calculate starting value of x:
    status = 1
    values_of_v_and_v_cubed = [(9, 729), (8, 512), (7, 343), (6, 216),
                               (5, 125), (4, 64), (3, 27), (2, 8), (1, 1)]
    for v,v_cubed in values_of_v_and_v_cubed :
        if n >= v_cubed :
            status = 0 ; break
    if status :
        # This should not happen.
        print (thisName, 'Internal error 4.')
        return None

    if n == v_cubed :
        x = v # Exact.
    else :
        # Newton's method:
        x = v + 1 ; y = x**3 - n
        status = 1 ; values_of_x = []
        if print_all :
            print (thisName)
            end_ = 0

        for t in range (1,51) :
            if print_all :
                if end_ : print ()
                print ('  x =', x)
                print ('  y =', y)
                end_ = 1
            slope = 3*x*x
            delta_x = y/slope
            x -= delta_x
            if x in values_of_x[-1:-5:-1] :
                # This value of x has been used previously.
                status = 0
                break
            values_of_x += [x]
            y = x*x*x - n

        if print_all : print ('  count =', t)
        if status :
            # This should not happen.
            print (thisName, 'count expired.')
            return None

    multiplier1 = (1,-1)[bool(sign1)]
    exponent1, remainder = divmod (exponent, 3)
    multiplier2 = 10**dD(exponent1)

    root3 = (multiplier1 * x * multiplier2).normalize() # The cube root.

    if check :
        dgt.prec = desired_precision
        n1 = root3 ** 3
        dgt.prec = Precision
        if (n1 != dD(str(N))) :
            print (thisName, 'Internal error 5.')
            print ('  N  =', N)
            print ('  n1 =', n1)
            return None
    if print_ :
        print (thisName)
        print ('  Output = N ** (1/3) =', root3 )

    return root3

Examples

(-49.430863)^(⅓)

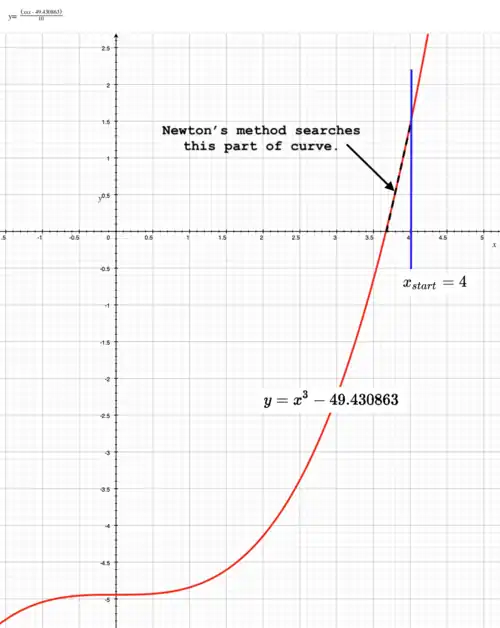
Graph of cubic function used to calculate cube root of $N=-49.430863.$

Y

axis compressed for clarity.
Method calculates

{\sqrt[{3}]{{\text{abs}}(-49.430863)}}.

1000>49.430863\geq 1,

therefore

n=49.430863

and negative sign

(-)

is preserved.
Newton's method quickly finds result:

3.67={\sqrt[{3}]{49.430863}}.

# python code.

NormalizeNumberDebug = 8
N = -49.430863
r = simpleCubeRoot (N, 2)
print ('\nCube root of {} = {}'.format(N,r))

simpleCubeRoot () :
  Input N = -49.430863
  flag_ = 0b10 
simpleCubeRoot () :
  sign1 = 1 
  n = 49.430863
  exponent = 0 
simpleCubeRoot () :
  x = 4
  y = 14.569137
  
  x = 3.6964763125
  y = 1.077556932370513542983642578125
  
  x = 3.670189185975939771448945836039493832417954712178864798200343445074621595436673614052572376229354069071
  y = 0.00764477504335853140747839082789084303615917679270634421640530090118268716447856580204634509997849803
  
  x = 3.670000009751736682821587362098730324894353971034852020032605567239509057372246925097634126721776189698
  y = 3.9403549966877805031675033177310279758144394720652549872722882467517684885827998893960547929841E-7
  
  x = 3.670000000000000025911816892145655551872936964331495318518061888183507160413379366174501446719474401728
  y = 1.04701101161586186758022322575610863475276107519253768435609331357966880617783675518439E-15

  x = 3.670000000000000000000000000000000182948843229450935510129377172924076310714715139745670785290354823955
  y = 7.39235902371945511587714470461319164277193070156347301951569000635639E-33
    
  x = 3.670000000000000000000000000000000000000000000000000000000000000000009119967095093791663852670429064766
  y = 3.6850777442132631162379569822609127E-67

  x = 3.670000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
  y = 0E-101
  count = 8 
simpleCubeRoot () :
  Output = N ** (1/3) = -3.67

Cube root of -49.430863 = -3.67

N small

# python code.

N = (dD('654.12345')**3)* dD('1e-234')
r = simpleCubeRoot (N, 2)
print ('\nCube root of',N,'=',r)

simpleCubeRoot () :
  Input N = 2.79884698523170070963625E-226
  flag_ = 0b10 
simpleCubeRoot () :
  sign1 = 0 
  n = 279.884698523170070963625
  exponent = -228 
simpleCubeRoot () :
  x = 7
  y = 63.115301476829929036375
  
  x = 6.570644207640612727643707482993197278911564625850340136054421768707482993197278911564625850340136054422
  y = 3.7921241319748044856346690723358910662200347438658510815125764506555202024351783380759402655041377003
  
  x = 6.541365939235037323691695638525121571862836044524137388147811941164515617543727416575923849380448976852
  y = 0.0168723059341306128289220155501386417560252058196372910481381594756277968737806202081810180585981468
  
  x = 6.541234502641062578339783186964860309131529958383953551860723864105607355316972754950658566210572503873
  y = 3.390153665112801204924990755018923043331713010875531529597912358746623245660302509054057497205E-7
  
  x = 6.541234500000000001066344822059465818454480153206314150749531142856041068525641678563938956757562592024
  y = 1.368794830901676242840644465509188865946206745677321533271630194477320979479731975131E-16

  x = 6.541234500000000000000000000000000000173834354896317173607861575067843889032458069846902551041303696479
  y = 2.23139421219918741184735707270203562908734282972217340770547002443E-35
    
  x = 6.541234500000000000000000000000000000000000000000000000000000000000000000004619675833700618822003921149
  y = 5.929965871075583921456016257E-73

  x = 6.541234500000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
  y = 0E-100
  count = 8 
simpleCubeRoot () :
  Output = N ** (1/3) = 6.5412345E-76

Cube root of 2.79884698523170070963625E-226 = 6.5412345E-76

N with 102 decimal digits

# python code.

desired_precision = 110
Precision = dgt.prec = desired_precision + 3     # Adjust as necessary.

N = dD('91234567890.12345678901234567890123')**3
r = simpleCubeRoot (N,2)
print ('''
Cube root of {}
  = {}'''.format(N,r))

simpleCubeRoot () :
  Input N = 759413404032709802223035921205529.781633123988862756497856617560063741408069807576943069432557725290867
  flag_ = 0b10
simpleCubeRoot () :
  sign1 = 0
  n = 759.413404032709802223035921205529781633123988862756497856617560063741408069807576943069432557725290867
  exponent = 30
simpleCubeRoot () :
  x = 10
  y = 240.586595967290197776964078794470218366876011137243502143382439936258591930192423056930567442274709133
  
  x = 9.1980446801090326740767864040184326054437466295425216595220585335458046935660252564768981085257509695566666666667
  y = 18.77820665551422495383824857173248095793272325233656814694510850270967196003505739741920782438368016883367944227
  
  x = 9.1240599949931623321664263546967588277013422167312019450898763745034405805394622722445816188927044087634255868627
  y = 0.15063796707487503447652546220546007622895104520340178579594123893590883076604801830026422013014041937608940920
  
  x = 9.1234568288903645757636608593967193590532344706953269357275443939995698575917750346229607570213472584647914653782
  y = 0.00000995803550427983012306112778540777688652481208248640053261156681610990067746729397462608294518324636155989
  
  x = 9.1234567890123458532053846994321774021465971937678169135851020569774194125848355752830106295283475121571096686441
  y = 4.352590615034382352966739799800228929244369059424641507909334544190744465475094678843434802753864E-14
  
  x = 9.1234567890123456789012345678901263300904970218124391473359075160634634033723697405398374188771027302554310464010
  y = 8.3156486139967105310855857875110175852544229130768260284187973010829718068550033E-31
  
  x = 9.1234567890123456789012345678901230000000000000000000000000000000012154935322004708306387167486681445055079073469
  y = 3.0352379658763986320970141849733835293969476411E-64
    
  x = 9.1234567890123456789012345678901230000000000000000000000000000000000000000000000000000000000000000000000000000000
  y = 0E-110
  count = 8 
simpleCubeRoot () :
  Output = N ** (1/3) = 91234567890.12345678901234567890123
  
Cube root of 759413404032709802223035921205529.781633123988862756497856617560063741408069807576943069432557725290867
  = 91234567890.12345678901234567890123

Result is achieved with 8 passes through loop.

In python this method is more than 3 times faster than raising a number to the power ${\frac {1}{3}}.$ As size of $N$ increases, speed advantage increases.

This method produced the cube root exactly.

For most invocations of function simpleCubeRoot () you probably don't want to see all the internal details as displayed above. However, it is

recommended that the function be invoked with flag = 4, because this value of flag causes execution of function to perform internal checking.

Links to related topics

Cubic formula

Square Roots using Newton’s Method

Shifting nth root algorithm

Powers, roots, and exponents

Roots

Exercises

This article is issued from Wikiversity. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.