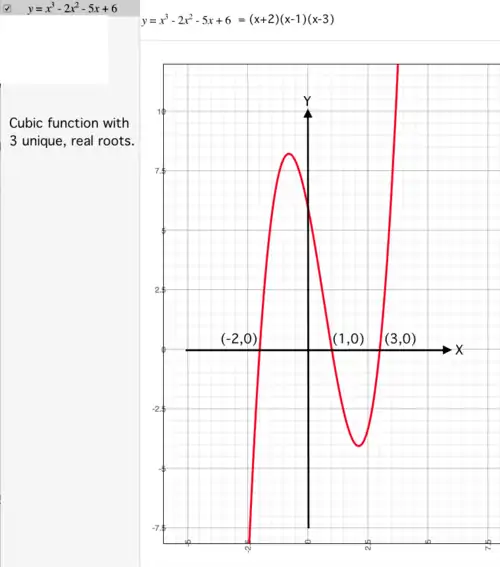
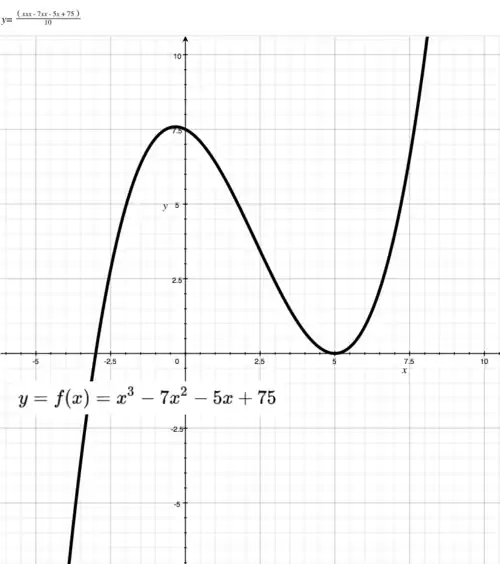
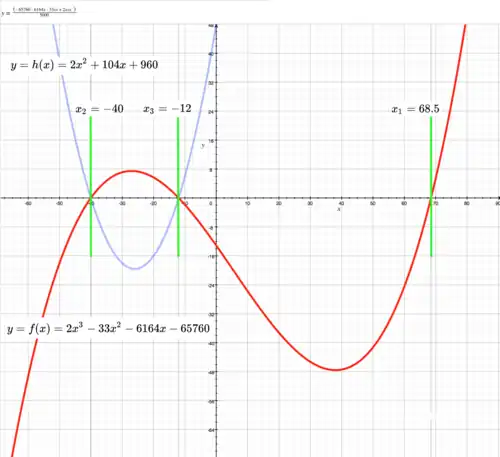
Cubic function
It is not the purpose of this page to repeat good information available elsewhere. However, it seems to the author that other descriptions of the cubic function are more complicated than they need to be. This page attempts to demystify elementary but essential information concerning the cubic function.
Objective

|
Lesson
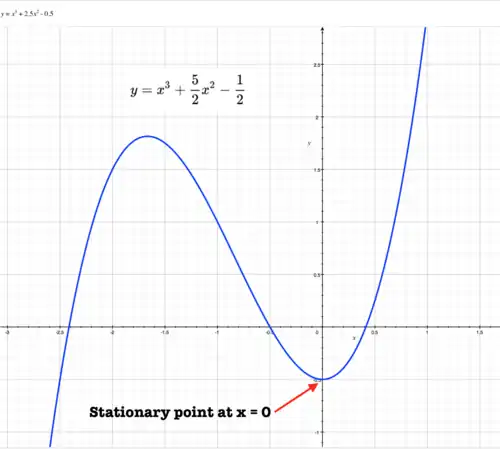
IntroductionThe cubic function is the sum of powers of from through :
usually written as:
If the function becomes Within this page we'll say that:
The cubic equation is the cubic function equated to zero: . Roots of the function are values of that satisfy the cubic equation. Because all coefficients must be real numbers, the cubic function must have 3 real roots or exactly 1 real root. Other combinations of real and complex roots are possible, but they produce complex coefficients. Characteristics of cubic functionsCoefficient c missing
x = f(y)
Coefficient a negative
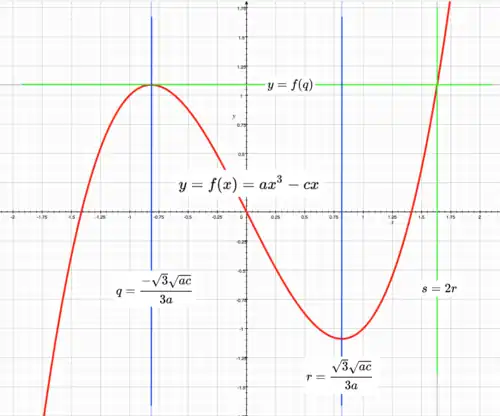
Sum of roots 0
Ratio of stationary points to roots
s = 2r
Function as product of 3 linear functionsThe function may be expressed as: where are roots of the function, in which case where: Solving the cubic equation means that, given , at least one of must be calculated. Given , I found that can be calculated as:
This approach was not helpful. Function as product of linear function and quadraticWhen is a root of the function, the function may be expressed as: where
When one real root is known, the other two roots may be calculated as roots of the quadratic function .
Function defined by 4 points
Function defined by 3 points and 1 slope
|
The simplest cubic function
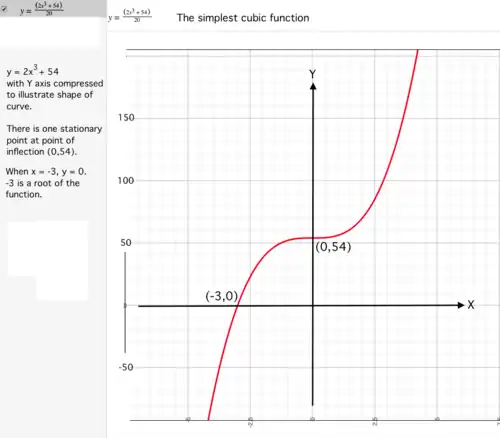 Figure 1. The simplest cubic function has coefficients The simplest cubic function has coefficients , for example: . To solve the equation:
The function also contains two complex roots that may be found as solutions of the associated quadratic:
This is equivalent to finding a root of function
Then Remember to preserve correct sign of result. |
Roots of equal absolute value
|
The cubic function Let one value of be and another be . Substitute these values into the original function in and expand.
Reduce and and substitute for :
Combine and to eliminate and produce a function in :
From If is a solution and function becomes:
and two roots of are . An example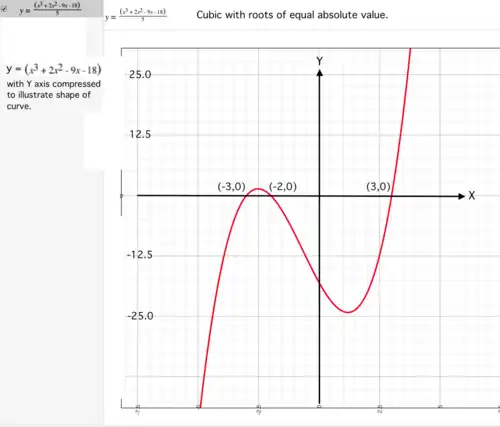 Figure 2. The roots of equal absolute value are See Figure 2.
The function has roots of equal absolute value.
The roots of equal absolute value are .
|
Equal Roots
|
Combine and from above to eliminate and produce a function in :
If because , there is a stationary point where .
and can be combined to produce:
ExamplesNo equal roots
Exactly 2 equal roots
3 equal roots
|
Depressed cubic
|
The depressed cubic may be used to solve the cubic equation. In the cubic function: let , substitute for and expand:
When the function is equated to , the depressed equation is: where and
In the depressed equation the coefficient of is and the coefficient of is .
Be prepared for the possibility that one or both of may be zero. 6 examples
When A = 0
When B = 0
When A = B = 0
|
Vieta's substitution
|
See Vieta's Substitution. Let the depressed cubic be written as: where and Let Substitute for in the depressed function:
where and . From the quadratic formula: The discriminant . Substitute for and expand: This discriminant = The factor is a factor of under "Equal Roots" above. Discriminant (B² - 4C³) == 0
Discriminant (B² - 4C³) positive
Discriminant (B² - 4C³) negative
|
Review of complex math
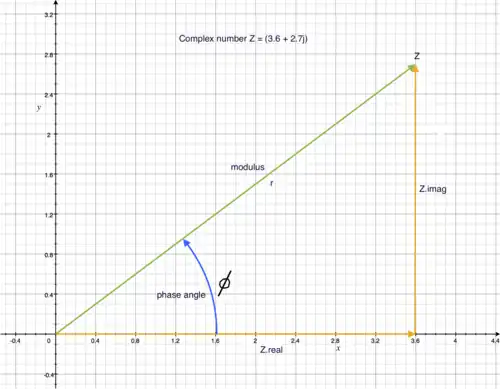 Figure 6a: Components of complex number Z. Origin at point . parallel to axis. parallel to axis. = modulus of Angle is the phase of
 Figure 6b: Complex numbers and . Origin at point . (off image to left.) A complex number contains a real part and an imaginary part, eg: In theoretical math the value is usually written as . In the field of electrical engineering and computer language Python it is usually written as .
The value is a complex number expressed in polar format where is the modulus of or and is the phase of or
Multiplication of complex numbers
To multiply complex numbers, multiply the moduli and add the phases. Complex number cubed
For the cube of a complex number in polar format, Cube root of complex number WLet and If then: and
Complex number w + C/wLet where
If
In the case of 3 real roots, |
Cubic formula
|
The substitutions made above can be used to produce a formula for the solution of the cubic equation. Given cubic equation: calculate the 3 values of where:
Using cubic formula
|
cos (A/3)
|
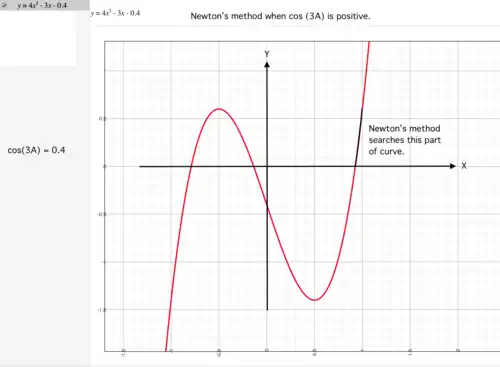
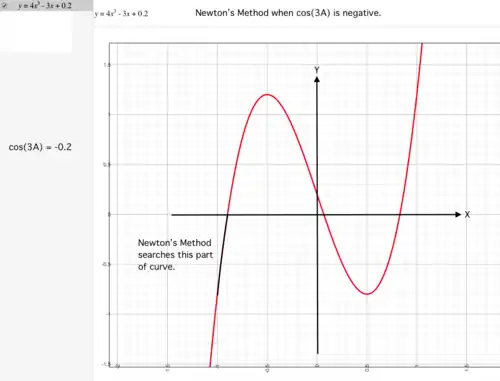
The method above for calculating depends upon calculating the value of angle However, may be calculated from because Generally, when is known, there are 3 possible values of the third angle because This suggests that there is a cubic relationship between and Expansion of cos (3A)
Newton's Method
|
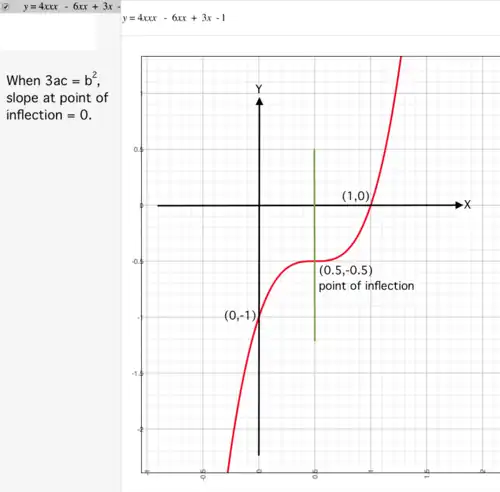
Point of Inflection
|
The Point of Inflection is the point at which the slope of the curve is minimum. After taking the first and second derivatives value at point of inflection is:
The slope at point of inflection is:
Value at point of inflection is:
From basic principles
Depressed cubicRecall from "Depressed cubic" above:
Therefore:
If 1 of is zero, the cubic equation may be solved as under "Depressed cubic" above. |
Newton's Method
|
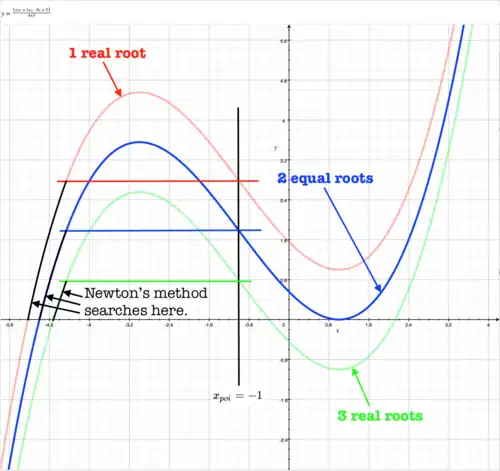
If both of the depressed function are non-zero, Newton's method may be applied to the original cubic function, and the Point of Inflection offers a convenient starting point.
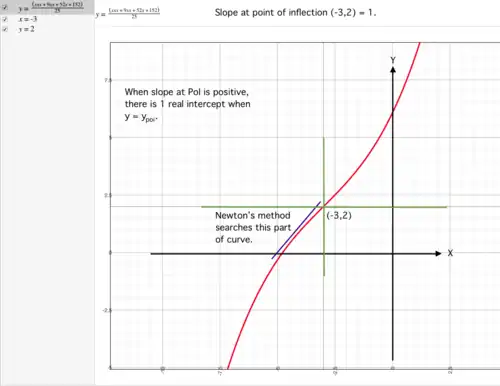
slope at PoI positive
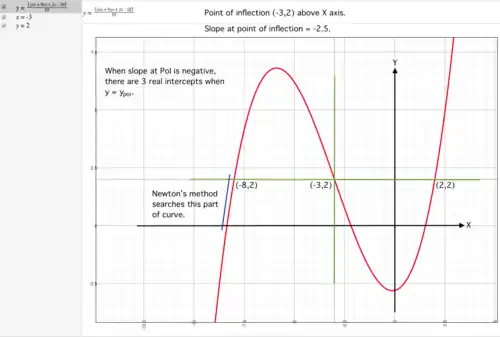
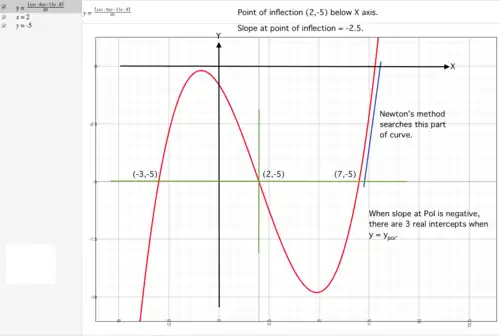
slope at PoI negative
Using Newton's method
In practice
|
Translation of axes
Cubic function relative to (u,v)

Graphs of 2 cubic functions with same shape.
Red curve relative to point is same as blue curve relative to The familiar equation of the cubic function: This is the equation of relative to origin However, need not be constrained as always relative to origin. It is always possible, and sometimes desirable, to express relative to any other point in the two dimensional plane. The process of producing a new function that is relative to is called "Translation of axes." On this page the point of reference of any cubic function is the point of inflection.
|
Move cubic function to (u,v)
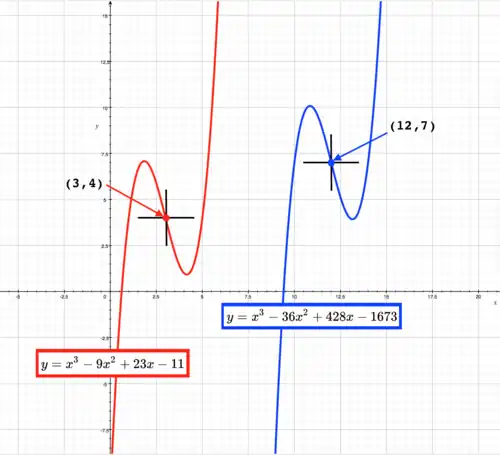
Graphs of 2 cubic functions with same shape.
Red curve moved to has equation Blue curve moved to has equation When a cubic function is moved to point the point of inflection is moved from present position to and the amount of movement is:
or where:
|
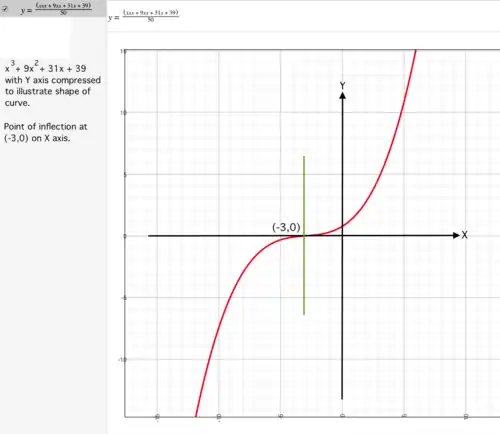
Describing a cubic function

Graph of complicated cubic function simplified.
Given a random cubic function, particularly those with large coefficients, it's usually difficult to visualize the function. One way to simplify our perception of a random cubic function is to consider the function at origin This can be done by:
Consider function Point of inflection is Equation of relative to point of inflection is: See red curve in diagram. may be described as moved to point |